Ответы
Ответ дал:
2
Ответ:
n принадлежит Z.
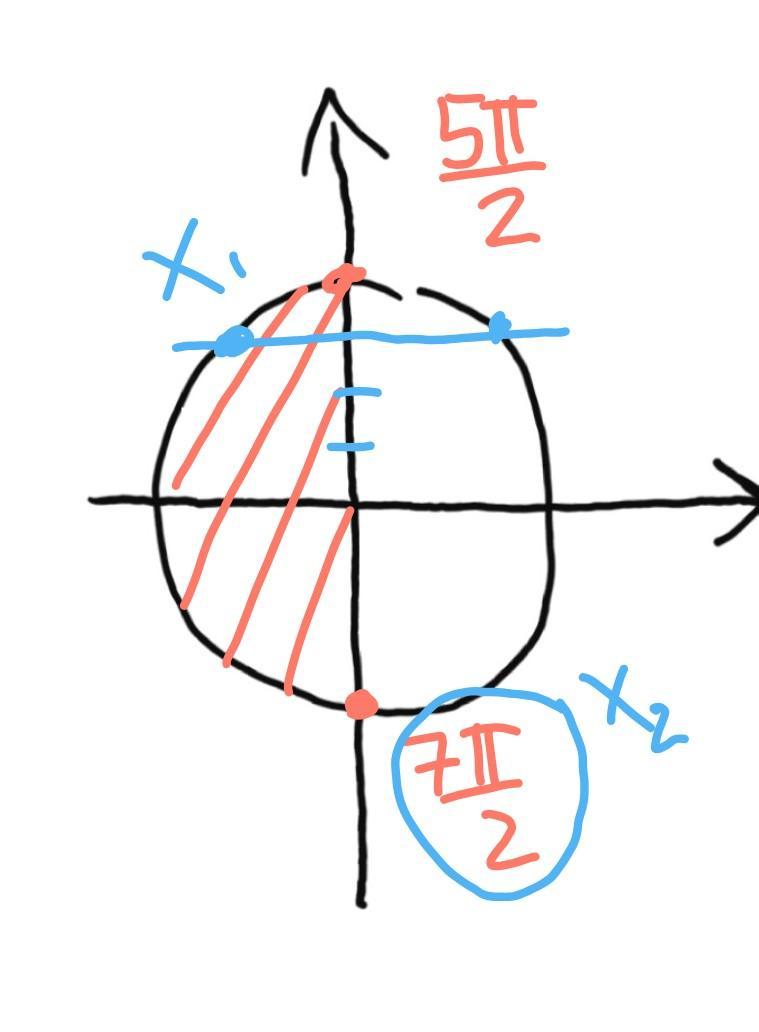
На промежутке:
рисунок
Приложения:
mliiiii:
Вы - лучшее, что случилось со мной
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад
