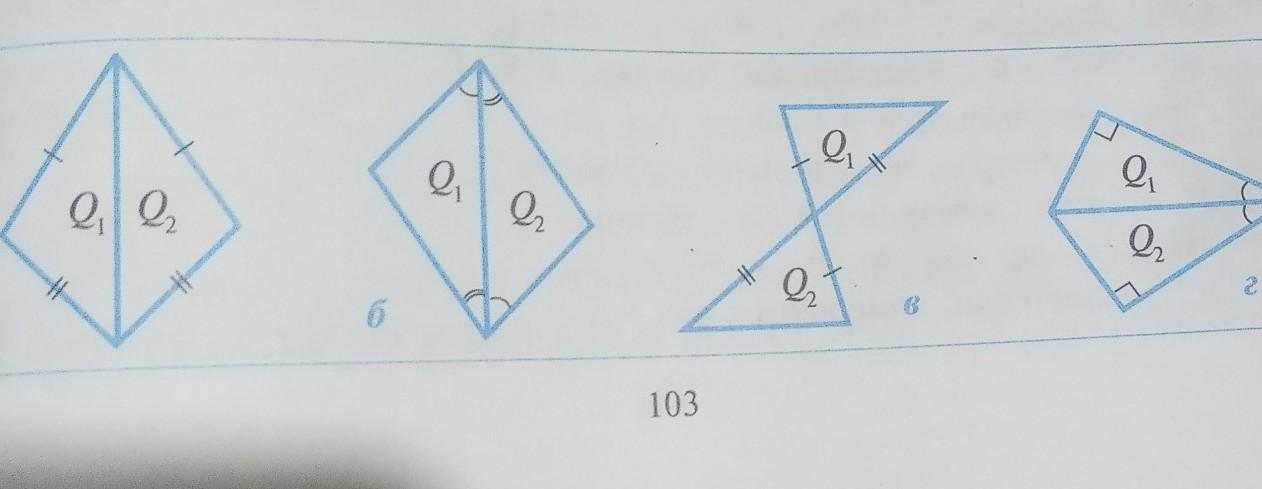
Ответы
Ответ дал:
3
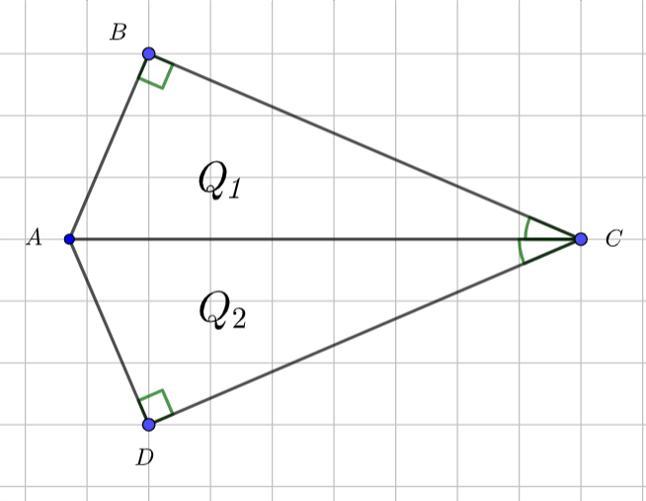
Ответ: ΔQ₁ = ΔQ₂ по гипотенузе и острому углу.
Объяснение:
Обозначим верхний треугольник как ABC, нижний — как ADC.
Тогда ∠ABC = 90°; ∠ADC = 90°; ∠BCA = ∠DCA.
Нужно доказать, что ΔABC = ΔADC.
Доказательство:
ΔABC и ΔADC — прямоугольные.
Гипотенуза AC у них общая.
∠BCA = ∠DCA (по условию).
Признак равенства прямоугольных треугольников:
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то эти треугольники равны.
Значит, ΔABC = ΔADC (по гипотенузе и острому углу).
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад