Question

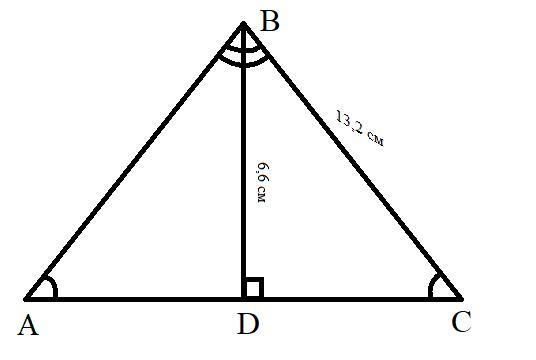
В равнобедренном треугольнике ABC проведена высота BD к основанию AC.
Длина высоты — 6,6 см, длина боковой стороны — 13,2 см.
Определи углы этого треугольника.

∡ BAC = °;

∡ BCA = °;

∡ ABC = °.

Answer 1

ротив катета ВД лежат углы А и С, поэтому угол А и С равны по 30°, так как по условию гипотенуза - боковая сторона в два раза больше катета ВД - высоты. /12.4/6.2=2/

∡BAC= 30° ∡BCA= 30° ∡ABC= 120° /180°-30°-30°/

Answer 2

(Смотри вложение)

1)Найдём ∠ BCD

$\displaystyle sin BCD =\frac{6,6}{13,2} =\frac{1}{2}$

Мы знаем, что синус 30° = 0,5, значит ∠ BCD = 30°

Т.к. Наш треугольник равнобедренный ⇒ ∠ BAD = ∠ BCD = 30°

2) Сумма всех углов в треугольнике = 180°

∠ ABC = 180° - (∠ BAD + ∠ BCD) = 180° - (30°+30°) = 120°

Ответ: ∠ BAD = 30°, ∠ BCD = 30°,  ∠ ABC = 120°