Question

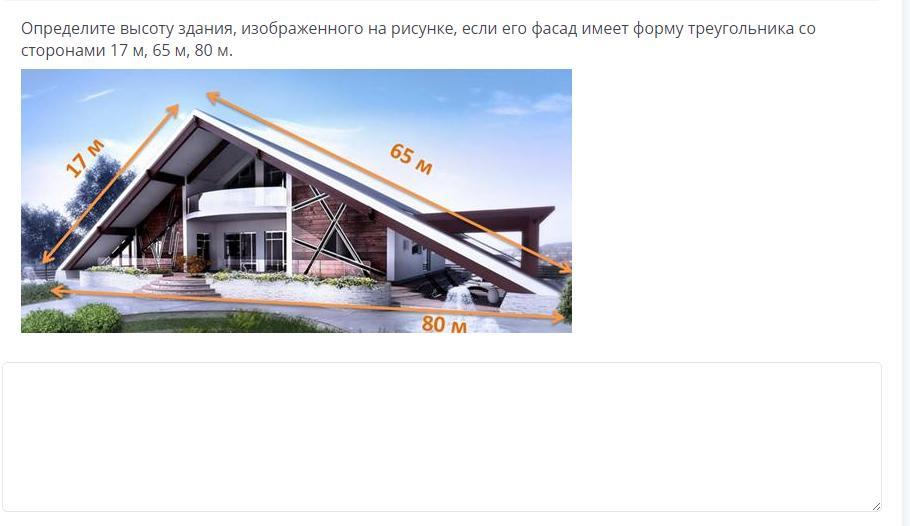
Определите высоту здания, изображенного на рисунке, если его фасад имеет форму треугольника со сторонами 17 м, 65 м, 80 м.
Помогите с сором по геометрии пожалуйста

Answer 1

Ответ:

Высота здания 7,2 м

Объяснение:

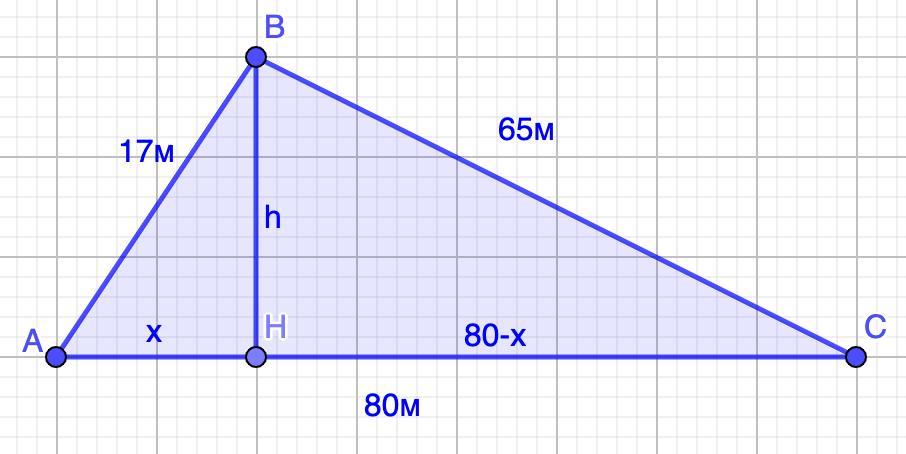
Дано: ΔАВС

АВ=17 м; ВС=65 м; АС=80 м.

Найти: h

Решение:

Проведем высоту ВН=h.

Рассмотрим ΔАВН  - прямоугольный.

Пусть АН=х.

Выразим h по теореме Пифагора:

h²=АВ²-АН² ⇒ h²=17²-x²    (1)

Рассмотрим ΔНВС  - прямоугольный.

Если АН=х, то НС=80-х.

Выразим h по теореме Пифагора:

h²=ВС²-НС² ⇒ h²=65²-(80-х)²     (2)

Из выражений (1) и (2) имеем:

17²-х²=65²-(80-х)²

289-х²=4225-6400+160х-х²

160х=2464

х=15,4

То есть АН=15,4 м

Теперь из (1) найдем h:

h²=17²-15,4²

h²=51,84

h=7,2

Высота здания 7,2 м.

Answer 2

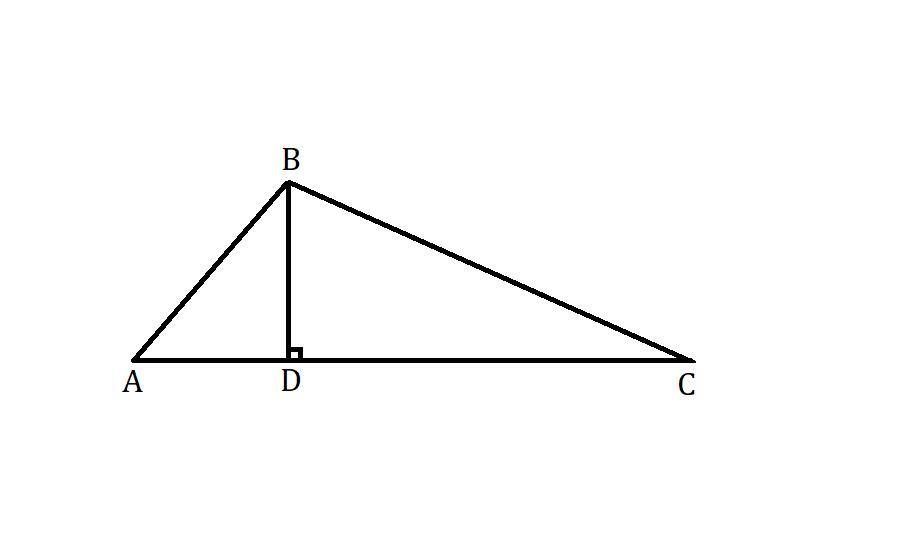
Дано:

ΔABC;

BD - выcота;

AB = 17 м;

BC = 65 м;

AC = 80 м.

Найти:

BD.

Решение:

Воспользуемся 2-мя формулами нахождения площади треугольника:

$\bf S = \sqrt{p(p-AB)(p-BC)(p-AC)}$

$\bf p = \dfrac{AB + BC + AC}{2} = \dfrac{17+65+80}{2} = 81$ м

$\bf S = \dfrac{AC * BD}{2}$

Пусть x м - BD.

$\bf \sqrt{81*(81-17)(81-65)(81-80)} = \dfrac{80*x}{2}$

$\bf \sqrt{81 * 64*16*1} = x * 40$

$\bf 9 * 8 * 4 = 40x$

$\bf 288 = 40x$

$\bf x = 288 : 40$

$\bf x = 7,2$

Ответ: 7,2 м