Question

В прямоугольной трапеции диагональ является биссектрисой острого угла. Найдите площадь трапеции, если боковые стороны равны 6 см и 12 см

Answer 1

Ответ:

103,2 см²

Объяснение:

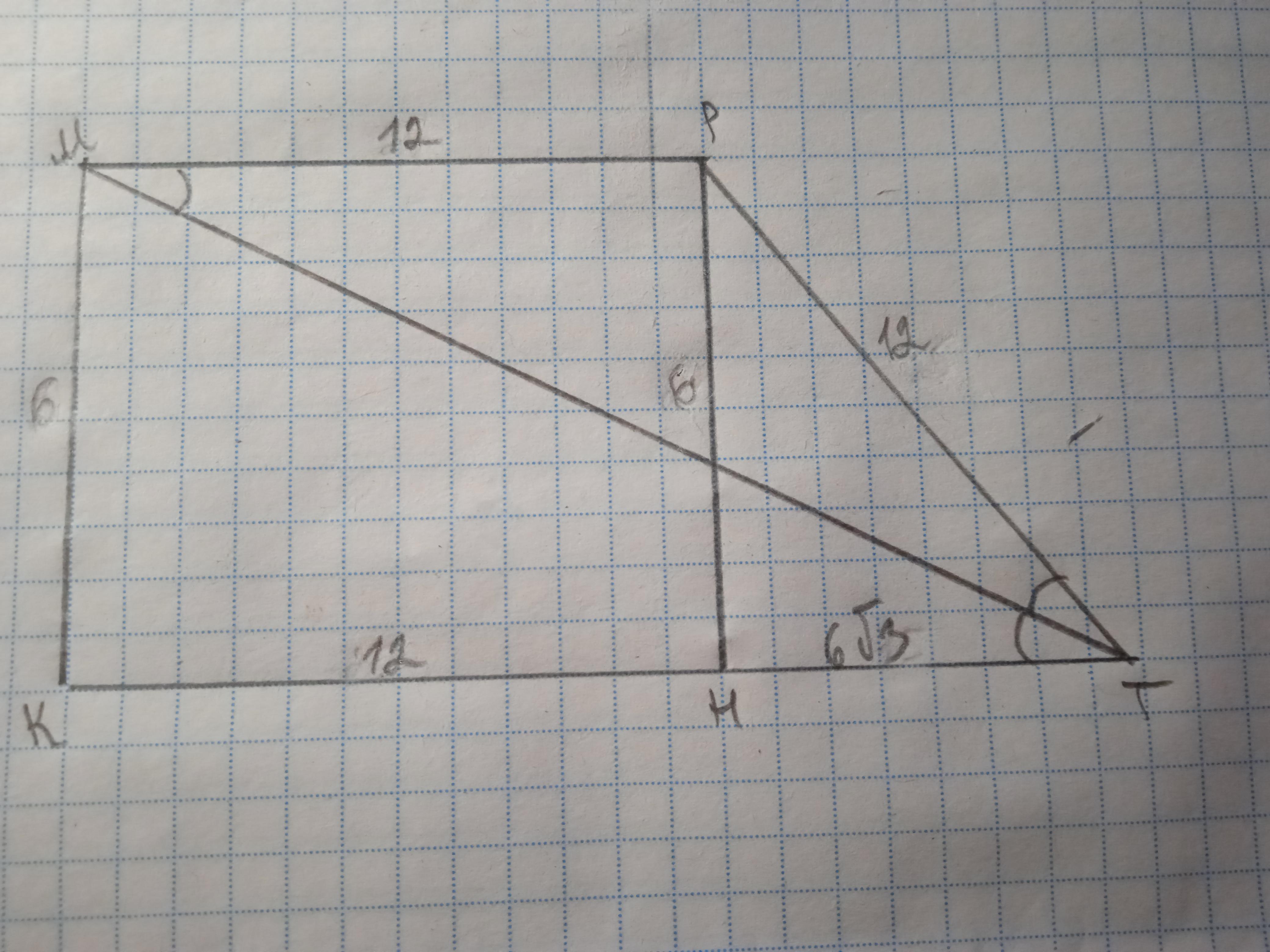
Дано: КМРТ - трапеция, МК⊥КТ,  МК=6 см,  РТ=12 см.  МТ - биссектриса. Найти S(КМРТ).

∠КТМ=∠РТМ по определению биссектрисы

∠РМТ=∠МТК как внутренние накрест лежащие при МР║КТ и секущей МТ, значит ΔМРТ - равнобедренный, МР=РТ=12 см.

Проведем высоту РН=МК=6 см.

КН=МР=12 см.

ΔРТН - прямоугольный, РТ=12 см, РН=6 см, значит по теореме Пифагора   ТН=√(144-36)=√108≈10.4 см

КТ=КН+ТН=12+10.4≈22,4 см.

S=(МР+КТ):2*РН≈(12+22,4):2*6≈103,2 см²