Ответы
Ответ дал:
1
Ответ: ∠COZ=92
Объяснение: ∠OCZ=180-∠VCZ ∠OCZ=180-130=50
∠OCZ+∠CZO+∠COZ=180
(x+8)+(3x+2)+50=180
4x=120 x=30 ⇒ ∠COZ=3x+2=3*30+2=92
Ответ дал:
1
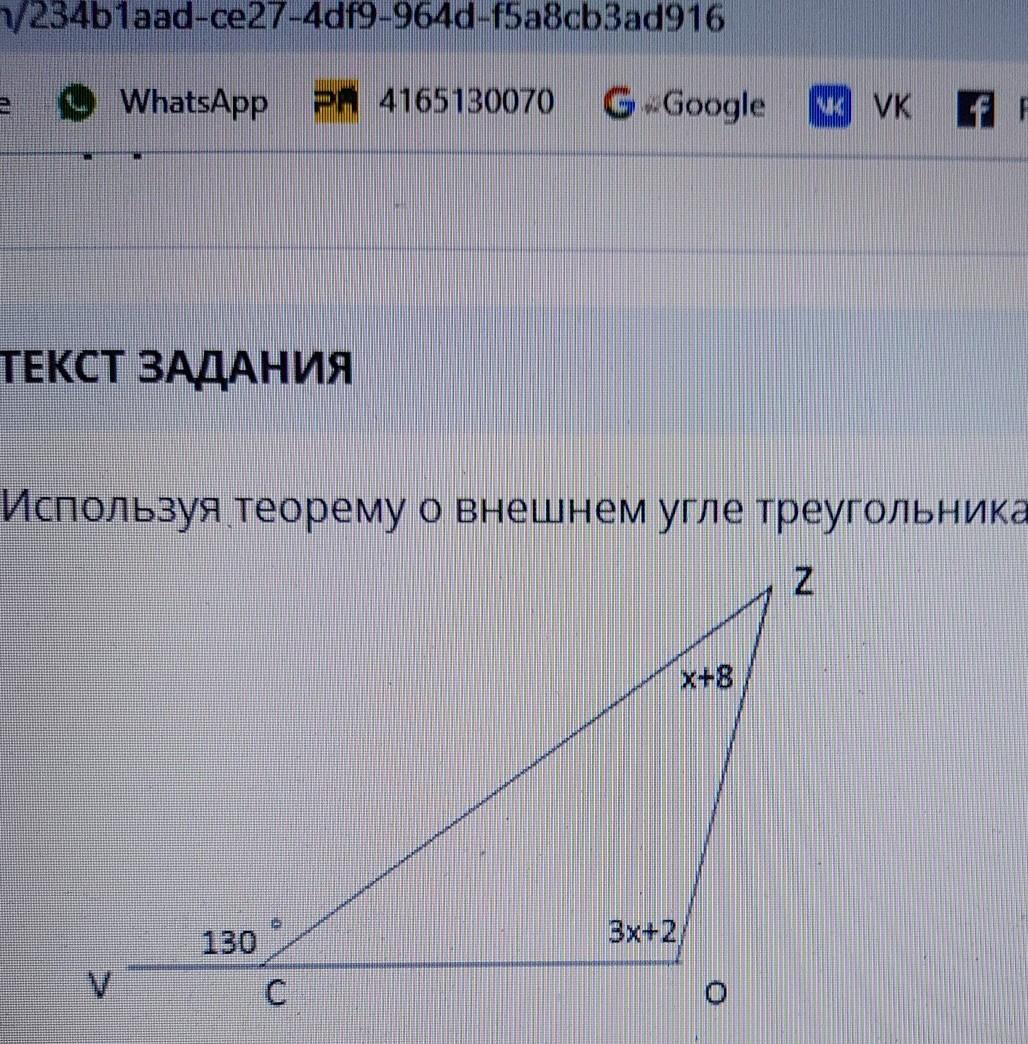
Теорема о внешнем угле треугольника:
"Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом".
∠О + ∠Z = ∠VCZ
(3x+2°) + (x+8°) = 130°
4x + 10° = 130°
4x = 130° - 10°
4x = 120°
x = 120° : 4
x = 30°
∠O = 3x+2°
∠O = 3 · 30° + 2° = 92°
∠O = 92°
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад