Question

ОЧЕНЬ СРОЧНО!!!! Помогите пожалуйста с геометрией (9 класс)!!!! Тут 2 номера!

Answer 1

2. Формула радиуса вписанной окружности в правильном шестиугольнике такова:

$r = \frac{\sqrt3}{2}a$

a = 12 => : $r = \frac{\sqrt3}{2}12 => r = 10.392.$

3. Доказать: $R = 2r.$

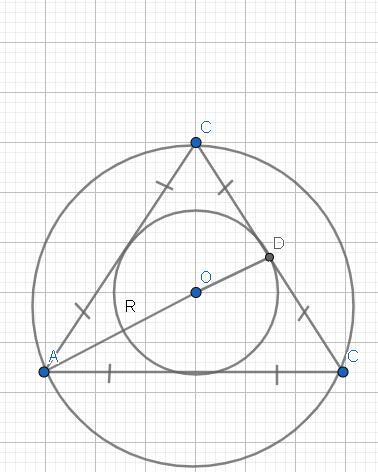
У нас есть правильный треугольник, со сторонами: AC == AB == BC.

Опишем вокруг этого треугольника окружность, чей радиус — R․

Дальше мы вписываем окружность в треугольнике ΔABC.

Так как треугольник ровносторонний, тоесть правильный — то центр описанной окружности совпадает с центром вписанной окружности.

В нашем случае, центр вписанной него окружности лежит в точке пересечения всех медиан.

И в точке пересечения — медианы делятся в отношении 2:1, что и означает: AO = 2OD => R = 2r.