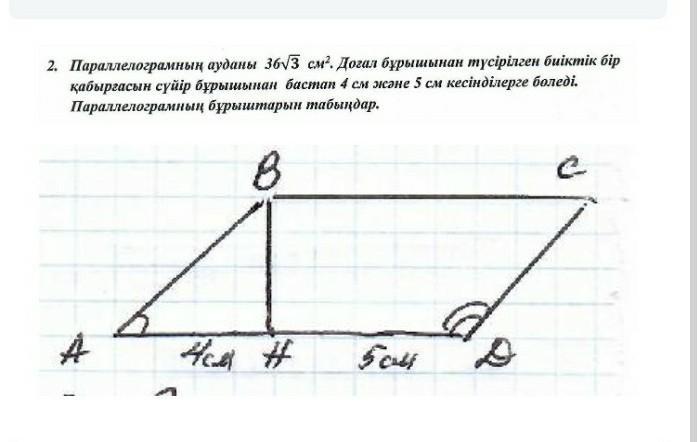
Площадь параллелограмма 36/3 см. Высота, взятая от тупого угла, разделяет одну стену на секции 4 см и 5 см от острого угла. Найдите углы параллелограмма.

Приложения:

Ответы

Ответ дал: bityukovps

Ответ:

60° и 120°

Объяснение:

S = AD*BH

BH = 36√3 : (5+4) = 4√3

в прямоугольном Δ ABH отношение BH к AH это тангенс ∠А. Находим arctg:

arctg 4√3 / 4 = arctg √3 = 60°

Тупой угол будет равен 180 - 60 = 120°

Аноним: это правильно ?

bityukovps: Если вы арккосинусы еще не проходили, то можно решить через вычисление гипотенузы в треугольнике ABH по Теореме Пифагора. Корень из суммы катетов получается 8. По одному из свойств прямоугольного треугольника катет AH вдвое меньше гипотенузы АВ, значит он лежит напротив угла 30. Соответственно угол А равен 60.

Вас заинтересует

Русский язык

2 года назад

Выпишите слово в котором правоописание н и нн в суффиксе является исключением из правила немцы предлагали советские солдатам, захваченным в здании сельсовета, сохранить жизнь, если они положат

Русский язык

2 года назад

В2 прошу срочно прошу

Английский язык

2 года назад

СРОЧНО, ПОМОГИТЕ, ПОЖАЛУЙСТА=*)))))))))) 1. A severe lack of rainfall can often lead to... а) flooding б) hurricane в) drought

Русский язык

2 года назад