Ответы
Ответ:
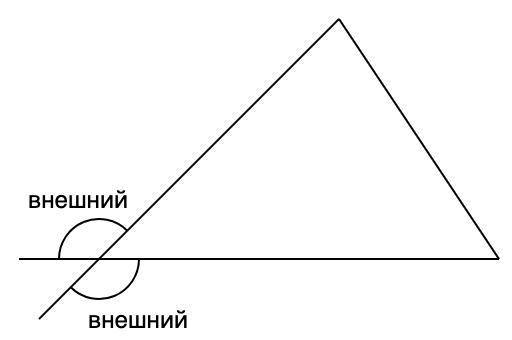
1)Внешний угол треугольника (многоугольника) - угол, образованный одной из его сторон и продолжением смежной стороны
2)Теорема
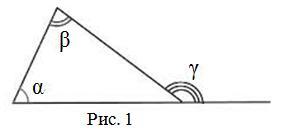
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним:
∠γ=∠α+∠β
(рис.1)
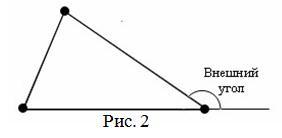
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине (внутренним углом) (рис. 2).
Следствие
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
3) Сумма смежных угов равна 180° ⇒ 180°-120°=60°-один внутренний угол; 180°-135°=45°-второй внутренний угол.Сумма углов в треугольнике равна 180° ⇒ 180°-45°-60°=75°-третий внутренний угол
Ответ:Внутренние углы в треугольнике: 60°, 45°, 75°
Объяснение:
1. Внешним называется угол, смежный с одним из углов треугольника. Сторонами внешнего угла являются сторона треугольника и продолжение другой стороны треугольника (см. рис.).
2. Внешний угол равен треугольника равен сумме двух других углов этого треугольника, не смежных с данным внешним углом.
3. Обозначим внутренние углы треугольника как A, B и C. Пусть указанные в задаче внешние углы смежны с A и B. Тогда можно записать систему из трех уравнений:
120° = B + C (по теореме о внешнем угле)
135° = A + C (по теореме о внешнем угле)
180° = A + B + C (т.к. сумма уголов треугольника всегда равна 180°)
Вычитая из третьего уравнения первые два, получаем:
180° – 135° – 120° = A + B + C – A – C – B – C ⇔ C = 75°
Подставляя C в первое уравнение: 120° = B + 75° ⇔ B = 45°
Подставляя C во второе уравнение: 135° = A + 75° ⇔ A = 60°
Ответ: углы треугольника A = 60°, B = 45°, C = 75°.