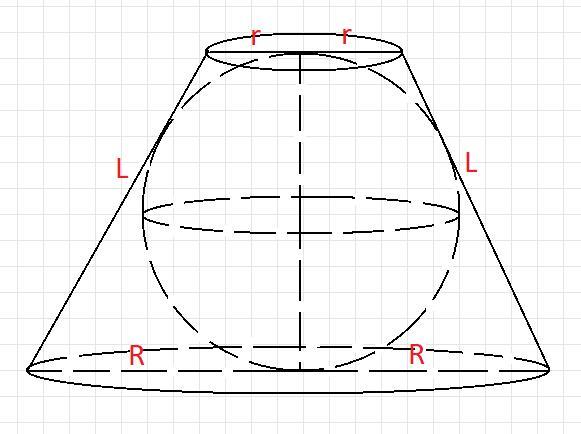
В усеченный конус с радиусами оснований R и r вписан шар. Найдите длину образующей усеченного конуса.
Ответы
Ответ дал:
4
Ответ:
L = r + R
Объяснение:
Рисунок к задаче смотри на фото.
Если в данном усеченном конусе проведем осевое сечение, то получим в сечении равнобедренную трапецию и вписанную в нее окружность.
В этой трапеции длина верхнего основания будет равна 2r, длина нижнего основания - 2R, длина боковой стороны - L (образующая конуса).
Если в четырехугольник вписана окружность, значит суммы его противоположных сторон равны.
2r + 2R = L + L
2L = 2(r + R)
L = r + R
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад