0. Доведіть, що середини сторін рівнобедреного
трикутника є вершинами також рівнобедреного
трикутника.
Ответы
Ответ дал:
3
Ответ:
Объяснение:
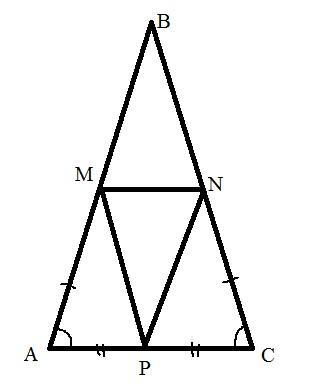
Пусть △ABC - равнобедренный, с боковыми сторонами АВ и ВС, а точки M, N, P - середины соответственно сторон АВ, ВС и АС.
△ABC - равнобедренный, значит АВ=ВС, и тогда АМ=МВ=BN=NC. Из этого равенства возьмём АМ=NC.
AP=PC, так как Р - середина АС.
<MAP=<NCP, так как △ABC - равнобедренный.
Значит △AMP=△CNP по 1му признаку. => MP=NP, а значит △MPN - равнобедренный, чтд.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад