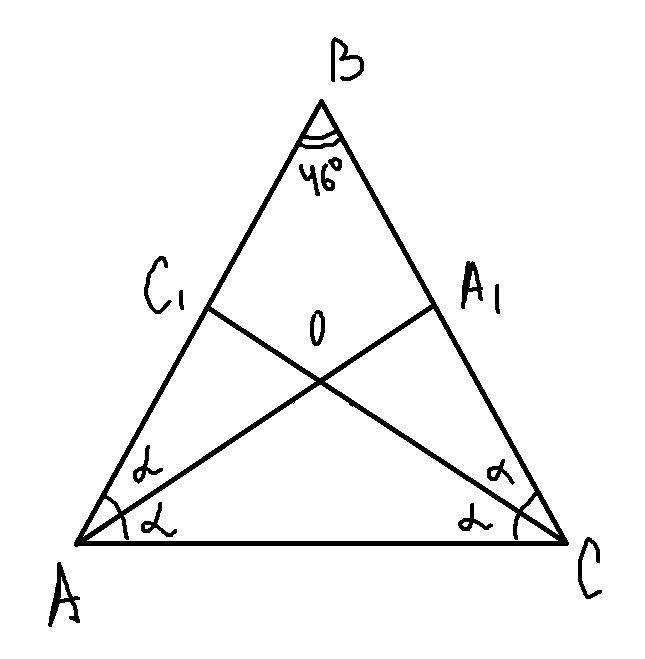
Произвольный треугольник имеет два равных угла. Третий угол в этом треугольнике равен 46°. Из равных углов проведены биссектрисы. Найди меньший угол, который образовывается при пересечении этих биссектрис.
Ответ: меньший угол равен °.
Ответы
Ответ дал:
4
(К решению идёт вложение)
1) Обозначим угол, разделённый биссектрисой как α, тогда ∠BAA₁=∠OAC=∠BCC₁=∠OCA=α
2) В треугольнике АВС
∠A+∠C+46°=180° ⇒ 2α+2α=134° ⇒ α=33,5°
3) Рассмотрим треугольник АСО
α+α+∠АОС=180° ⇒ ∠АОС=180°-67° = 113°
∠АОС = ∠А₁ОС₁ т.к. вертикальные ⇒∠АОС = ∠А₁ОС₁= 113°
4)∠А₁ОС =180°-∠А₁ОС₁ Т.к. ∠А₁ОС₁ и ∠А₁ОС - смежные
∠А₁ОС =180°-113°=67°
Ответ: меньший угол равен 67°.
Приложения:
ZefirkaIzi:
а чему равен большой угол
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад