Question

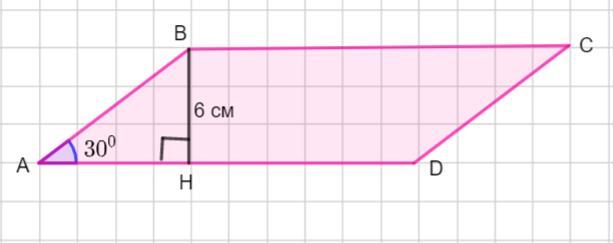
Периметр параллелограмма равен 54см. Найдите площадь параллелограмма, если его высота равна 6 см, а один из углов на 60° меньше прямого.

Answer 1

Ответ:

Площадь параллелограмма равна 90 см².

Объяснение:

По условию задан параллелограмм ABCD.

Пусть ∠ А на 60° меньше прямого.

Тогда найдем градусную меру ∠А.

∠А= 90°-60° =30°.

Проведем высоту параллелограмма ВН.

ВН =6 см.

Рассмотрим Δ АВН - прямоугольный, в нем ∠А=30°, а противолежащий катет ВН =6 см.

По свойству катета, лежащего напротив угла в 30°, гипотенуза АВ будет в 2 раза больше этого катета.

$AB= 2\cdot BH;\\AB=2\cdot6=12$

Тогда одна сторона параллелограмма равна 12 см.  Периметр параллелограмма - это сумма длин всех сторон параллелограмма.

Так как периметр параллелограмма равен 54 см, то найдем другую сторону параллелограмма.

$54:2-12 =27-12=15$ см.

Значит, AD=BC =15 см.

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

$S= AD\cdot BH;\\S= 15\cdot 6=90$

Площадь параллелограмма равна 90 см².