Question

СПАСАЙТЕ СОР ПО ГЕОМЕТРИИ ПЖЖЖЖ ПОСЛЕДНИЕ БАЛЫ
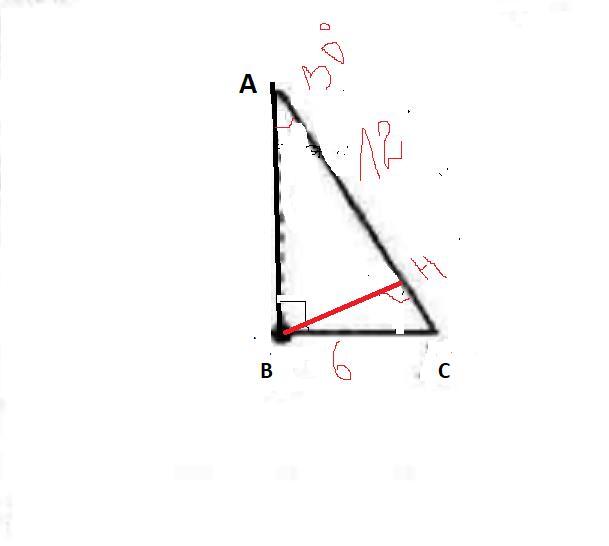
№4. В прямоугольном треугольнике АВС В90 0 , АВ =6 см, АС=12 см. Найдите углы,
которые образует высота ВН с катетами треугольника.

Answer 1

Ответ:

∠НВА=60°, ∠НВС=30°

Решение:

Дано:

ΔАВС, ∠В=90°, АС=12 см, АВ=6, ВН- высота

Найти: ∠НВС-? ∠НВА-?

Решение:

в ΔАВС

sin A= AB/AC;

sin A= 1/2

∠A=30°

По теореме о сумме острых углов Δ:

∠С=90°-30°=60°

В ΔНВА, ∠Н=90°, ∠А=30°.

По теореме о сумме острых углов Δ

∠НВА=90°-30°=60°

В ΔНВС, ∠Н=90°,∠С=60°

По теореме о сумме острых углов Δ

∠НВС=90°-60°=30°