помогите срочно очень нужно и быстро
Приложения:
filana85:
Кажется, 27⁰
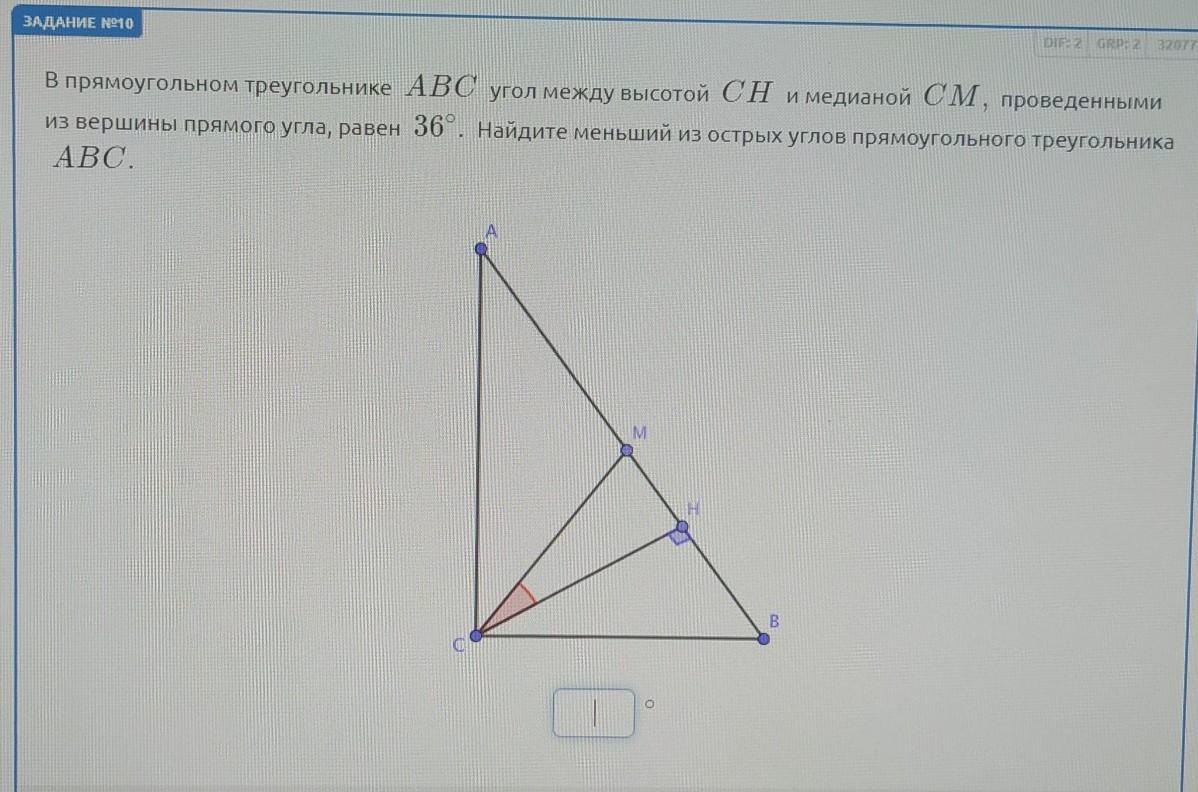
Угол СМН=180⁰-(90⁰+36⁰)=54⁰
Угол СМА=180⁰-54⁰=126⁰
Медиана в прямоугольном треугольнике равна половине гипотенузы. А это значит, что СМ=АМ. Следовательно треугольник АМС - равнобедренный
Угол А =(180⁰-126⁰)÷2=27⁰
Всё правильно.
Ответы
Ответ дал:
1
Ответ:
Меньший из острых углов прямоугольного треугольника АВС ∠ А = 27°.
Объяснение:
В прямоугольном треугольнике медиана равна половине гипотенузы.
Следовательно, треугольники АСМ и СМВ являются равнобедренными.
∠СМН = 90 - 36 = 54°, следовательно, ∠А = ∠АСМ = 54 : 2 = 27° (так как внешний угол треугольника равен сумме двух других углов, не смежных с ним).
∠В = 90 - ∠А = 90 - 27 = 63°.
Таким образом, меньший из острых углов прямоугольного треугольника АВС ∠ А = 27°.
Ответ: меньший из острых углов прямоугольного треугольника АВС ∠ А = 27°.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад