Question

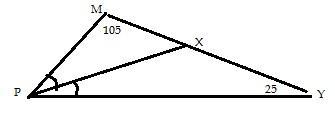
3. Биссектриса угла P треугольника MPУ пересекает сторону МУ точке Х.Угол
М= 105°, угол У= 25°.
www
А) Определите вид треугольника РХУ;
В) Сравните отрезки MX и XУ.

Answer 1

Ответ:

Объяснение:

1. ∠ХРУ = 50/2 = 25°, т.к. РУ - биссектриса

Δ РХУ - равнобедренный, т.к. его углы при основании РУ равны.

2. Поскольку биссектриса треугольника делит третью сторону на отрезки, пропорциональные двум другим прилежащим сторонам, сравним РМ и РУ.   По теореме о соотношении сторон и углов треугольника, напротив бОльшего угла лежит бОльшая сторона. РУ лежит напротив ∠105°. РМ - напротив угла 25° ⇒ РУ > РМ ⇒ ХУ, как прилежащая к РУ >  МХ, прилежащей к РМ.