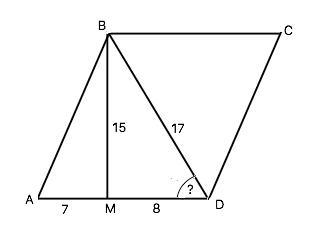
На стороне АД параллелограмма АВСД взята точка М так, что АМ=7см, МД =8 см, ВМ=15 см, ВД=17 см. Найдите площадь параллелограмма
Аноним:
Братан
Ты сделал? Можешь помочь
Ответы
Ответ дал:
38
Ответ: 225 см²
Объяснение:
Диагональ делит параллелограмм на два равных треугольника. Площадь каждого равна половине площади параллелограмма.
Одна из формул площади треугольника Ѕ=a•b•sinα, где а и b- стороны, α- угол между ними.
По т.косинусов соѕ(ВDА)=(ВМ²-BD²-MD²):2MD•DB ⇒
соѕ(∠BDM)=(225-289-64):272≈0, 470588.
По таблице или с помощью калькулятора найдем величину и затем синус этого угла ( угол ≈ 61,927°, синус ≈0,8824)=>
Ѕ(ABCD)=2S(ABD)=2•17•(7+8)•0,8824=225,012≈225 см².
——————
Решение будет значительно проще и короче, если вспомнить, что треугольник со сторонами 15, 8 и 17 – из Пифагоровых троек и является прямоугольным ( проверьте по т.Пифагора). Тогда ВМ - высота параллелограмма и
Ѕ(ABCD)=BM•AD=15•15=225 см²
Приложения:
а точно все правильно ?
а точно все правильно ?
а точно все правильно ?
Разберите внимательно и не спеша запись решения, чтобы понять его. Тогда обязательно поймете, правильное оно или нет.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад