Ответы
Ответ:
В решении.
Пошаговое объяснение:
4. Найти целые решения системы неравенств:
2,8х - 17 > 0,3x - 4,5
12,3x - 16,6 <= 7,1x + 19,8
2,8x - 0,3x > -4,5 + 17
12,3x - 7,1 <= 19,8 + 16,6
2,5x > 12,5
5,2x <= 36,4
x > 12,5/2,5
x <= 36,4/5,2
x > 5
x <= 7
Решение первого неравенства х∈(5; +∞);
Решение второго неравенства х∈(-∞; 7];
Решение системы неравенств х∈(5; 7], пересечение.
Целые решения системы неравенств: 6, 7.
Первое неравенство строгое, скобка круглая, второе нестрогое, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.
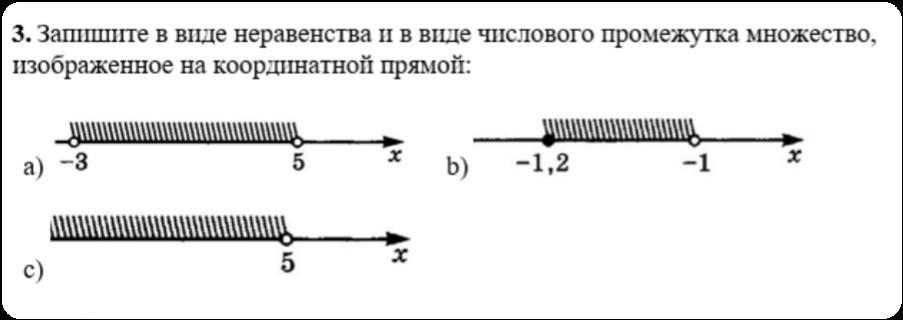
3.
а) -3 < x < 5; (-3; 5);
b) -1,2 < x < -1; [-1,2; -1);
c) -∞ < x < 5; (-∞; 5).
2. Начертить координатную прямую, отметить на ней -∞, -5, 1 и 7.
Первая штриховка: от -5 до 1, кружочки возле -5 и 1 закрашенные.
Вторая штриховка: от -∞ до 7, возле 7 кружочек закрашенный.
Пересечение [-5; 1], двойная штриховка.
Объединение (-∞; 7].
1. 5,6 <= a <= 5,8; 2,1 <= b <= 2,2.
a) Р = 2(а + b)
2(5,6 <= a <= 5,8)
+
(2,1 <= b <= 2,2)
=
2(7,7 <= a+b <= 8);
15,4<= P <= 16
b) S = a*b
5,6 <= a <= 5,8
умножить на
2,1 <= b <= 2,2
=
11,76 <= S <= 12,76.