Question

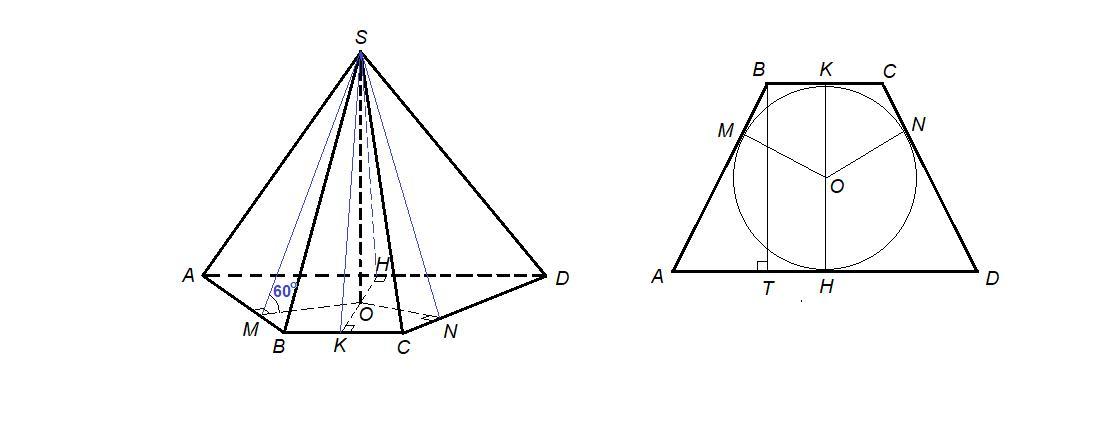
Основанием пирамиды является равнобокой трапеции, основания которой равны 4 см 16 см, а все двугранные углы пирамиды при ребра основания равны 60°. Найдите:
1)площадь боковой поверхности
2)второе высоту пирамиды.

Answer 1

Ответ:

1) 160 см²

2) 4√3 см

Объяснение:

• Если равны углы наклона боковых граней к плоскости основания (или равны высоты боковых граней), то высота пирамиды проецируется в центр окружности, вписанной в основание.

Докажем это.

Пусть SO - высота пирамиды.

Проведем ОК⊥BC, ОН⊥AD, ОМ⊥AB и ON⊥CD.

OK, OH, OM, ON - проекции соответствующих наклонных на плоскость основания, значит и наклонные перпендикулярны соответствующим сторонам основания по теореме о трех перпендикулярах.

∠SKO = ∠SHO = ∠SMO = ∠SNO = 60° - линейные углы наклона боковых граней к плоскости основания.

ΔSKO = ΔSHO = ΔSMO = ΔSNO по катету (SO - общий) и противолежащему острому углу, значит

SK = SH = SM = SN  и  OK = OH = OM = ON.

То есть точка О равноудалена от сторон основания, значит О - центр окружности, вписанной в основание.

• Если в четырехугольник можно вписать окружность, то суммы противолежащих сторон его равны.

AD + BC = AB + CD = 4 + 16 = 20 см

АВ = CD = 20 : 2 = 10 cм

Если ВТ высота, то по свойству равнобедренной трапеции:

AT = (AD - BC) : 2 = (16 - 4) : 2 = 6 см

ΔАВТ:  ∠АТВ = 90°, по теореме Пифагора

  ВТ = √(АВ² - АТ²) = √(10² - 6²) = √(100 - 36) = √64 = 8 см

Радиус вписанной в трапецию окружности равен половине высоты:

r = OM = 0,5 BT = 0,5 · 8 = 4 см

ΔSOM: ∠SOM = 90°,

 $\cos\angle SMO=\dfrac{OM}{SM}$

 $\dfrac{1}{2}=\dfrac{4}{SM}$

SM = 8 см

 $tg\angle SMO =\dfrac{SO}{OM}$

 $\sqrt{3}=\dfrac{SO}{4}$

 SO = 4√3 см - высота пирамиды

Так как высоты боковых граней равны, то площадь боковой поверхности можно найти по формуле:

Sбок. = 0,5 Pосн. · SM

Sбок. = 0,5 (4 + 16 + 10 + 10) · 8 = 160 см²