Question

в треугольнике abc угол c=90°,sinA=16/23,AC=√273.Найдите ab.

Answer 1

Ответ:

$\sin(A) = \frac{16}{23} \\ \\ \cos(A) = \sqrt{1 - \sin {}^{2} (A) } = \\ = \sqrt{1 - \frac{256}{529} } = \sqrt{ \frac{273}{529} } = \frac{ \sqrt{273} }{23} \\ \\ \cos(A) = \frac{AC}{AB} = \frac{ \sqrt{273} }{23} \\ \frac{ \sqrt{273} }{AB} = \frac{ \sqrt{273} }{23} \\ = > AB = 23$

Answer 2

Объяснение:

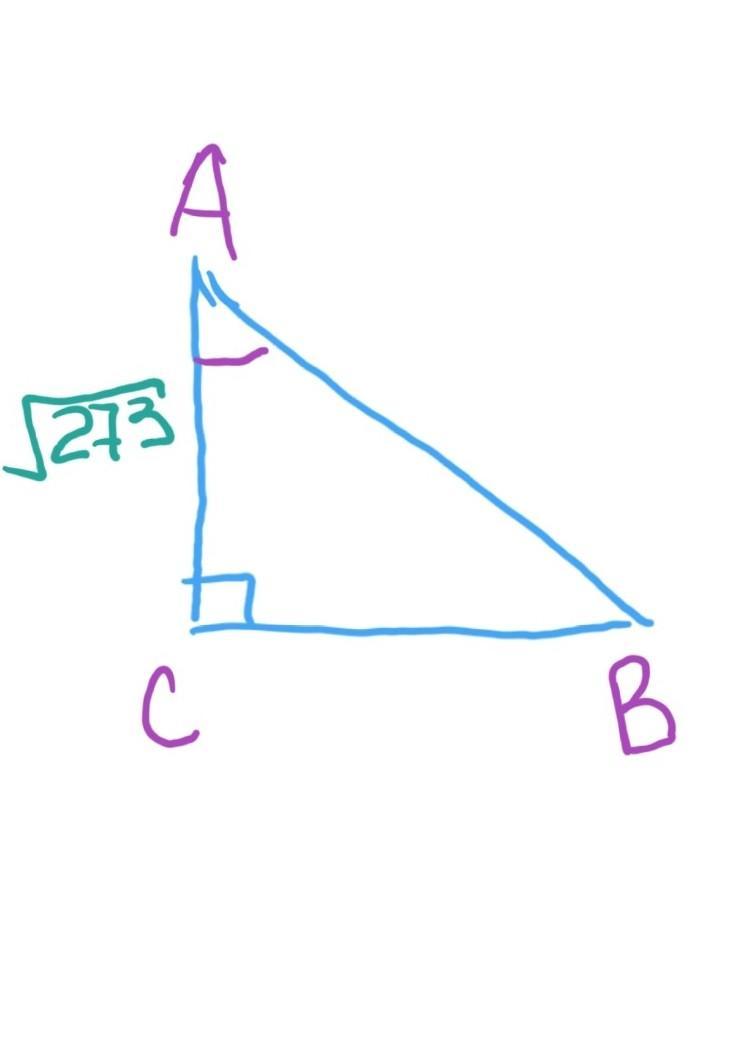
<C=90

sinA=16/23

AC=корень273

Найти : аb

cosA=AC/ab

ab=AC/cosA

cos^2(A)+sin^2(A)=1

cos^2(A)=1-sin^2(A)=1-(16/23)^2=

=1-256/529=(529-256)/529=273/529

cosA=корень273 /23

аb=корень273/ (корень273/23)=

=корен273 ×23/корень273=23

Ответ : ab=23