Question

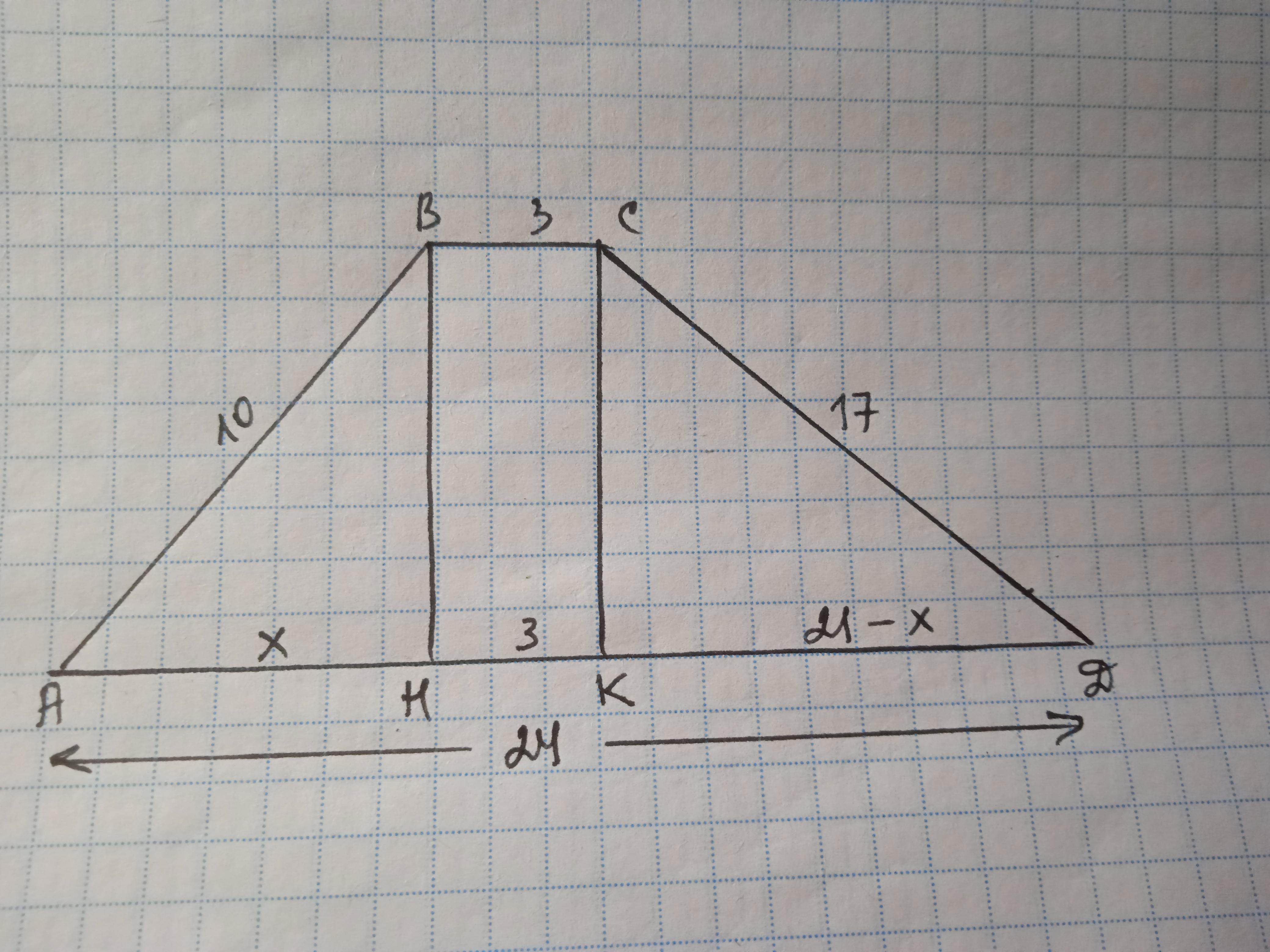
В трапеции ABCD (BC параллельна с AD) AB=10 BC=3,CD=17,AD=24.
Найдите площадь трапеции
ДАЮ 35 БАЛЛОВ​

Answer 1

Ответ:

108 см²

Объяснение:

Проведем высоты ВН и СК. КН=ВС=3 см;  АН+КD=24-3=21 см

Пусть АН=х см, тогда КD=21-х см.

По теореме Пифагора ВН²=АВ²-АН²;  СК=СD²-KD²

АВ²-АН²=СD²-KD²

100-х²=289-(21-х)²

100-х²-289+441-42х+х²=0

42х=252;  х=6

АН=6 см;  КD=21-6=15 cм

АD=6+3+15=24 см

ВН=√(100-36)=√64=8 см

S=(BC+AD):2*BH=(3+24):2*8=108 cм²