Question

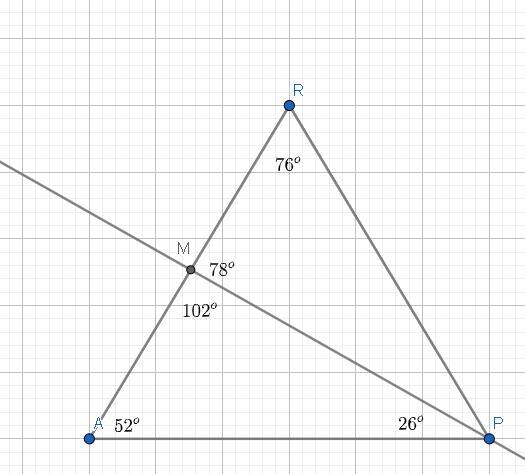
В равнобедренном треугольнике ARP проведена биссектриса PM угла P у основания AP,
∡ PMR = 78°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).
∡ A =


∡ P =


∡ R =



Помогитеее!!!!!!!!!

Answer 1

Так как биссектриса MP — делит угол <P на 2 равные части, то пусть половине этого угла будет (<MPA) объявлена как переменная "x".

А так как треугольник равнобёдренный, а AP — основание, то боковые стороны — AR & RP — равны, и их противоположные углы тоже.

Тоесть: <RAP == <RPA; <MPA = x ⇒ <RAP = 2x.

<RMP = 78° ⇒ <AMP = 180-78 = 102° (как смежные углы).

2x+x+102 = 180°

3x + 102 = 180°

3x = 180-102 ⇒ 3x = 78°

x = 78/3 = 26° ⇒ <MPA = 26°; <RAP = 26*2 = 52°.

<RAP == <RPA = 52° ⇒ <R = 180-(52+52) = 76°.

Вывод: <R = 76°; <A == <P = 52°