Срочно нужна помощь.
Нужно решить методом замены неопределенного интеграла
Приложения:
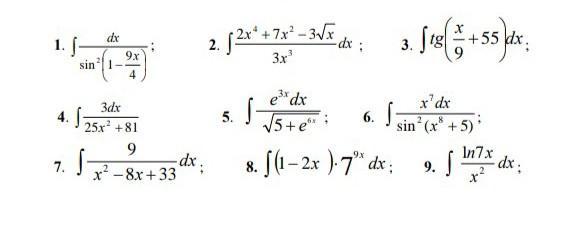
Miroslava227:
здесь только половина решается методом замены, остальное либо по частям, либо обычное интегрирование
Ответы
Ответ дал:
2
Ответ:
1.
2.
3.
4.
5.
6.
7.
8.
По частям:
9.
По частям:
Спасибо за помощь!)
Здравствуйте,простите,можете помочь?
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад