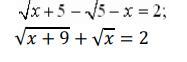Ответы
Ответ дал:
1
Ответ:
Нет корней;
Пошаговое объяснение:
ОДЗ:
Итого:
Решение:
Корень x=–4 не удовлетворяет ОДЗ.
Проверка:
Корень найден верно.
______________________________________________
ОДЗ:
Решение:
Проверка:
Полученный корень не обращает уравнение в верное равенство ⇒ корней нет.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад