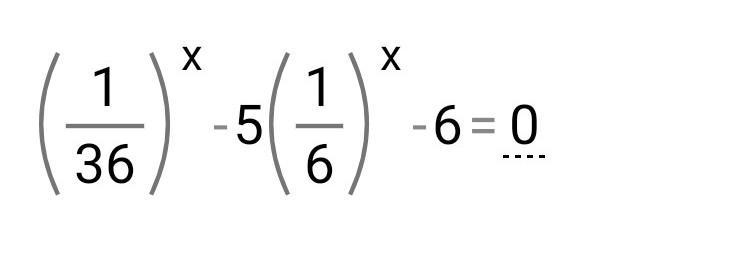Question

решите пж, это уравнение. срочно!​

Answer 1

/Ответ:

x=-1

Объяснение:

заметим, что 1/36=1/6², тогда

$((\frac{1}{6})^2)^x -5(\frac{1}{6})^x-6=0$, по свойству (a^n)^k=(a^n)^k, тогда

(1/6^2)^x=(1/6^x)^2. Сделаем замену (1/6^)x=t,t>0( по определению, показательная функция всегда больше нуля)

t²-5t-6=0. Решаем квадратное уравнения любым удобным способом

t=-1 не удовлетворяет условию, что t>0

t=6, тогда 1/6^x=6. представим 6 как 1/6 в степени минус 1, тогда

(1/6)^x=(1/6)^-1

Но если равны основания, то равны и показатели, следовательно

x=-1

Answer 2

${( \frac{1}{36} )}^{x} - 5 \times {( \frac{1}{6}) }^{x} - 6 = 0$

Пусть (1/6)^х = t,t>0,тогда

${t}^{2} - 5t - 6 = 0$

D = (-5)²-4*(-6) = 7²

$t1 = \frac{5 + 7}{2} = 6$

$t2 = \frac{5 - 7}{2} = - 1$

Вернёмся к замене:

Второй корень не подходит т.к. мы выставили условие t>0

Если (1/6)^х=6,то 6^(-х)=6¹ <=> -х=1 <=> х=-1

Ответ: х = -1