Question

ПОЖАЛУЙСТА ПОМОГИТЕ Я НЕ СПРАВЛЮСЬ САМ!
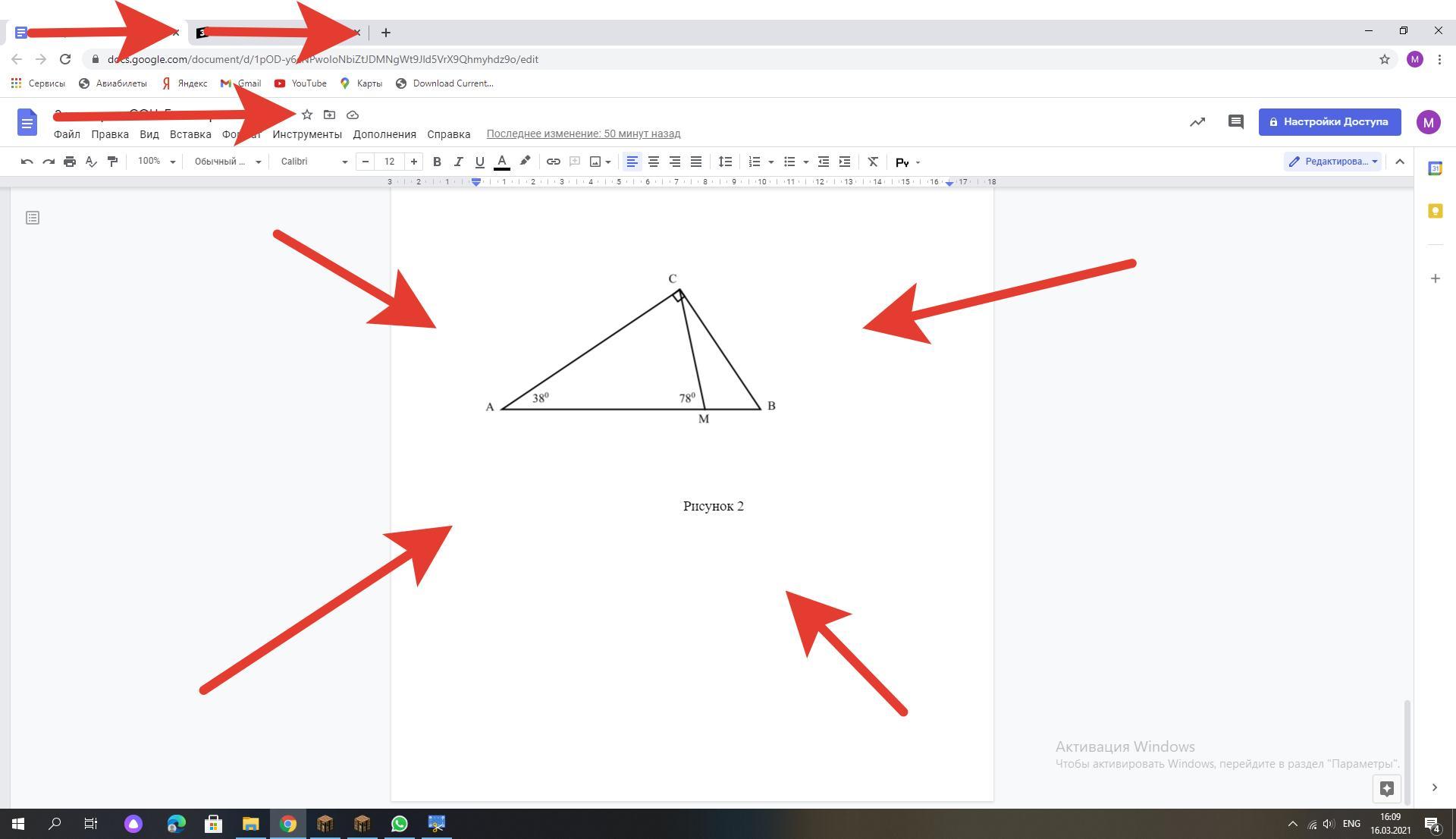
В прямоугольном треугольнике ABC (∠C=900) точка М лежит на гипотенузе AB, причем угол ∠CMA = 780. ∠А = 380. Докажите, что CB > CM
Рисунок внизуу

Answer 1

Ответ: 82°22  и 7°38±

Объяснение:   Расстояние от точки  до прямой  измеряется длиной отрезка, проведенного к данной прямой перпендикулярно. Из этого следует равенство ∆ АСМ и ∆ АКМ по катету (СМ=КМ) и общей гипотенузе АМ. Тогда угол САМ=угол КАМ. (см. приложенный рисунок).

    Из ∆ АСМ sin(СAМ)=CM/AM=2,7:4,1=>

sin (CAM)≈0,6585, что по калькулятору( и по таблице) соответствует углу 41,188°, откуда угол САВ=2•41,377° или 82°22´

Второй острый угол ∆ АВС=90°-82°22´=7°38´