Question

Один из углов равнобедренного тупоугольного треугольника на 102° больше другого.
Найдите больший угол этого треугольника. Ответ дайте в градусах.​

Answer 1

Ответ:

Больший угол треугольника равен 128°

Объяснение:

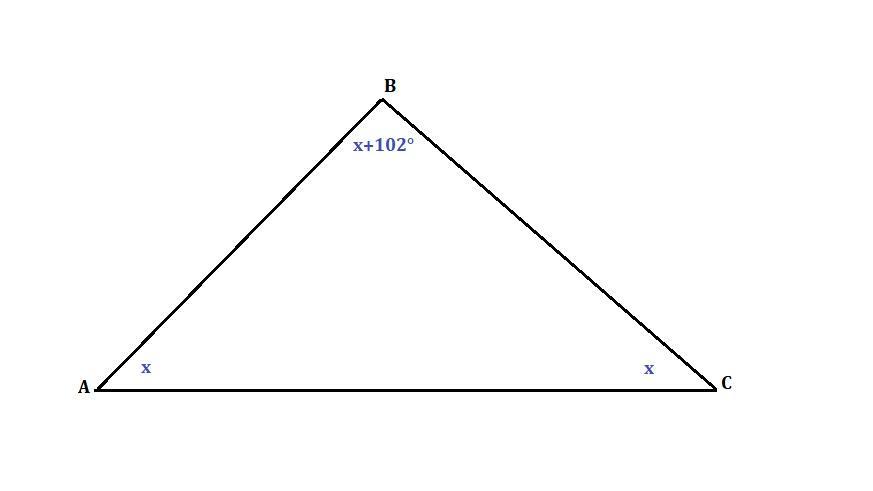
Рассмотрим равнобедренный треугольник АВС.

Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника.

Свойство равнобедренного треугольника: У равнобедренного  треугольника углы при его основании равны.

Пусть АС - основание ΔАВС. Боковые стороны АВ=ВС.

⇒∠А=∠С.

Так как сумма углов треугольника 180°, то два угла при его основе не могут быть тупыми ( >90° ). Поэтому обозначим углы при основе за х: ∠А=∠С=х. Тогда ∠В=х+102°.

Составляем уравнение:

∠А + ∠С + ∠В = 180°

х+х+х+102°=180°

3х=78°

х=26°

Тогда ∠В=х+102°=26°+102°=128°