Question

50б ПОМОГИИИИИИИИИИИИТЕ . Дан единичный куб ABCDA1B1C1D1. Найдите расстояния:
е) от точки D до плоскости AB1D1.

Answer 1

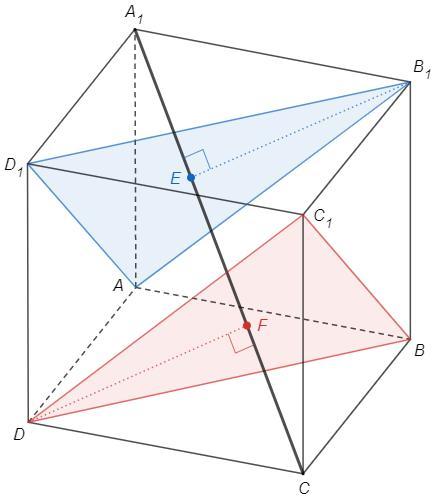
Диагонали противоположных граней куба параллельны.

AB1||DC1, D1B1||DB => (AB1D1)||(C1BD)

Достаточно найти расстояние между параллельными плоскостями.

A1AB1D1 и СAB1D1 - правильные пирамиды, вершины A1 и С проецируются в центр основания E.

То есть A1C⊥(AB1D1)

Аналогично A1C⊥(C1BD)

EF - искомое расстояние.

AB1 =√2 (диагональ квадрата)

B1E =√3/3 *AB1 =√6/3 (радиус описанной окружности правильного треугольника)

A1E =√(A1B1^2 -B1E^2) =√(1 -6/9) =√3/3

A1E =CF (высоты в равных пирамидах)

A1C =√3 (диагональ куба)

Таким образом EF =√3/3