Question

3. Дана функция: у=х² - 4х +3.
а) найдите точки пересечения графика с осьо ОУ:
b) найдите точки пересечения графика с осью ох;
с) запишите координаты вершины параболы;
d) запишите уравнение оси симметрии параболы:
е) постройте график функции
Срочно пожалуйста!!!!!

Answer 1

Ответ.

Построить график функции у = х² - 4х + 3, выполнить задания.

• Функция вида  f(x) = ax² + bx + c  - это квадратичная функция, ее графиком является парабола.

а) Найдем точки пересечения графика с осью ОУ.

График функции пресекает ось OY при условии: x = 0.
Точка с координатами (0; y) лежит на оси OY.

При x = 0 значение функции y = 0² - 4 · 0 + 3 =3.

График функции пересекает ось OY в точке (0; 3).

b) Найдем точки пересечения графика с осью OX.

График функции пресекает ось OX при условии: y = 0.
Точка с координатами (x; 0) лежит на оси OX.

При y = 0 решим квадратное уравнение.

х² - 4х + 3 = 0;

D = b² - 4ac = 4² - 4·3 = 16 - 12 = 4 = 2²;

$\displaystyle x_{1,2} =\frac{-b\pm\sqrt{D} }{2a} \\\\ \displaystyle x_{1} =\frac{-b-\sqrt{D} }{2a} = \frac{4-2}{2} = 1\\\\x_{2} =\frac{-b+\sqrt{D} }{2a} = \frac{4+2}{2} = \frac{6}{2} =3$

График функции пересекает ось OX в точках (1; 0) и (3; 0).

с) Запишем координаты вершины параболы (x₀; y₀).

$\displaystyle x_{0} = \frac {-b}{2a} = \frac{4}{2} =2;$

y₀ = 2² - 4 · 2 + 3 = 4 - 8 + 3 = -1.

Вершиной параболы является точка с координатами (2; -1).

d) Запишем уравнение оси симметрии параболы.

Ось симметрии параболы проходит через ее вершину параллельно оси OY.

Уравнение оси симметрии:
x = 2.

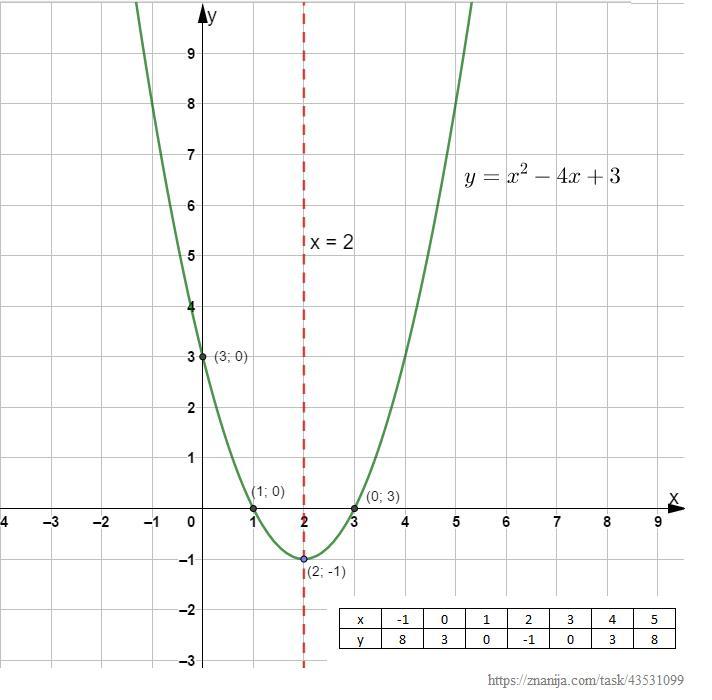
е) Построим график функции у = х² - 4х + 3.

Областью определения заданной функции является множество всех чисел.

D(f) = R.

Графиком данной квадратичной функции   у = х² - 4х + 3 является парабола.

Старший коэффициент a = 1,  a > 0. Ветви параболы направлены вверх.

Составим таблицу значений аргументов и значений функции.

x = -1; y = 1 + 4 + 3 = 8;

x = 0; y = 3;

x = 1; y = 0;

x = 2; y = -1; (вершина параболы)

x = 3; y = 0;

x = 4; y = 3 (точка симметрична точке (0; 3);

x = 5 y = 8  (точка симметрична точке (-1; 8).

Построим график.

(Прилагается).