35 БАЛОВ !!!!!!!
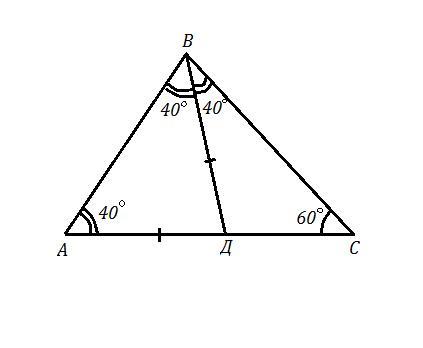
В треугольнике ABC проведена биссектриса BD угол A равен 40 градусов угол C равен 60 градусов
Докажите что треугольник BDA равнобедренный
Сравните отрезки AD и DC
Ответы
Ответ дал:
2
Ответ:
ΔАВС , ВД - биссектриса ⇒ ∠АВД=∠СВД , ∠А=40° ∠С=60° .
1) Так как ∠А+∠С=40°+60°=100° , то ∠В=180°-100°=80°
Так как ∠АВД=∠СВД , то они равны половине ∠В , то есть
∠АВД=∠СВД=40°
В ΔАВД: ∠А=∠АВД=40° (углы при основании треугольника равны) ⇒ ΔАВД - равнобедренный и АД=ВД .
Значит, ΔВДА ( что то же самое, что и ΔАВД) - равнобедренный , что и требовалось доказать .
2) АД > ДС
В треугольнике против бОльшего угла лежит бОльшая сторона, поэтому в ΔВСД : ВД > ДC , так как ∠СВД=40° , а ∠С=60° , против ∠СВД лежит сторона ДС , а против ∠С лежит сторона ВД .
Но из равнобедренного ΔАВД следует равенство сторон: ВД=АД .
Значит, если ВД > ДС и ВД=АД , то и АД >ДС .
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад