Похила утворює з площиною кут 30°. Знайдіть довжину похилої, якщо її проекція на площину дорівнює 4√3
Аноним:
cos30=4√3/х; х=2*4√3/√3=8
Ответы
Ответ дал:
0
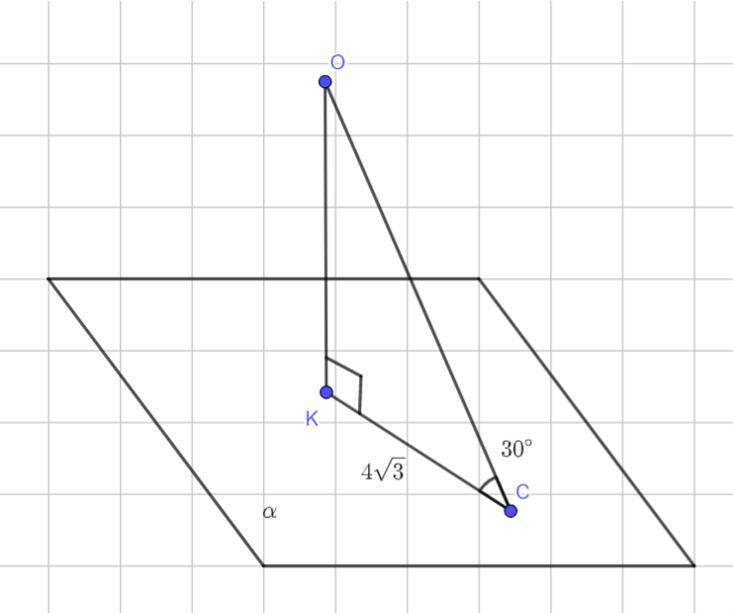
ОС — похила на площину α.
Проведемо перпендикуляр ОК до площини. KC = 4√3 — проекція похилої на площину α.
Кутом між прямою та площиною є кут між нею та її проекцією на цю площину, тож ∠OCK = 30°.
Так як ОК ⊥ α, то ОК ⊥ КС і ΔОКС є прямокутним.
За означенням косинуса гострого кута прямок. трикутника:
.
Виразимо звідси ОС і підставимо числові значення:
Відповідь: 8.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад