Question

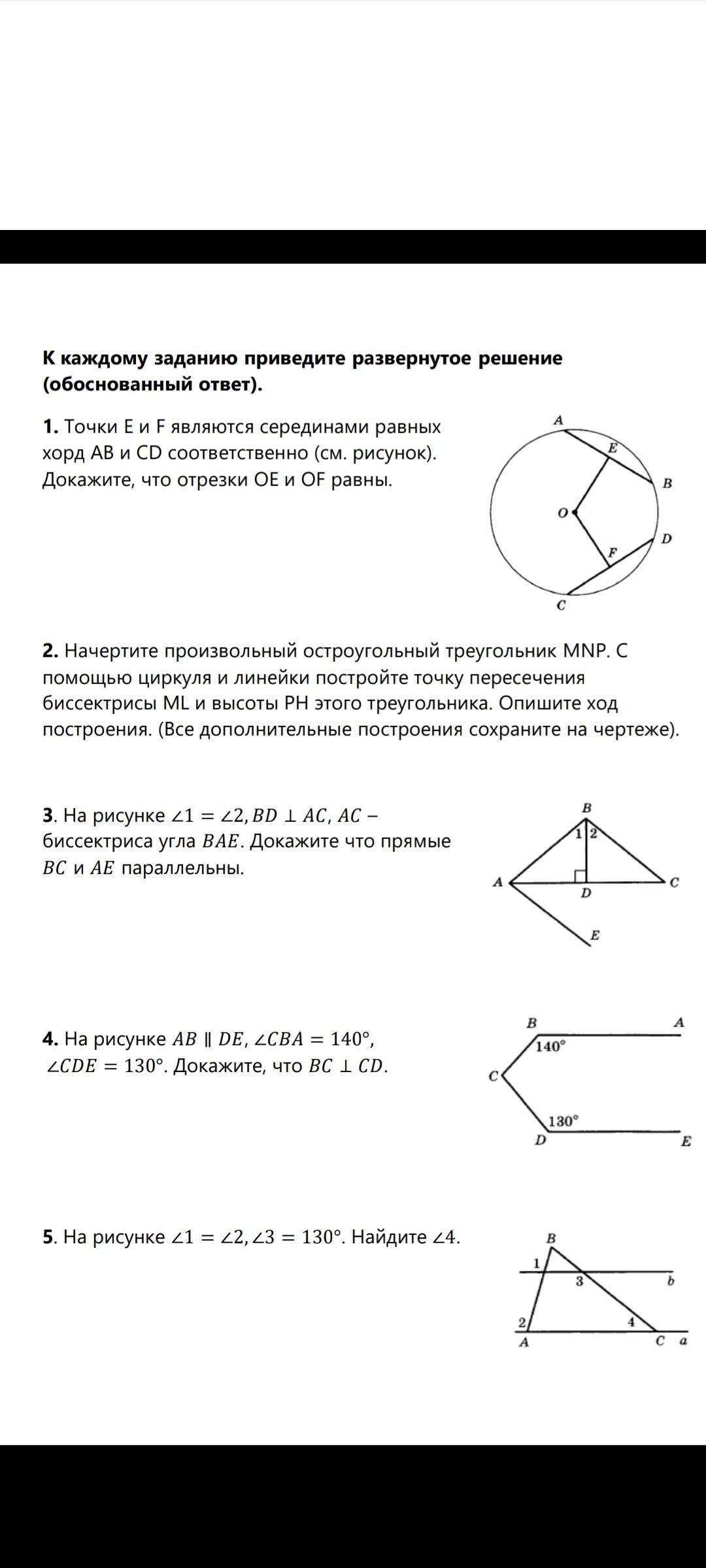
1. Точки E и F являются серединами равных
хорд AB и CD соответственно (см. рисунок).
Докажите, что отрезки OE и OF равны.

Answer 1

Ответ:

проведем радиусы CO, DO и AO, BO. Так как радиусы равны, и CD=AB по условию, значит треугольник AOB = треугольнику COD по трем сторонам, а так как OF и OE - медианы, значит они тоже равны, так как у равных треугольников равны биссектрисы, медианы, ср линии и т.д.