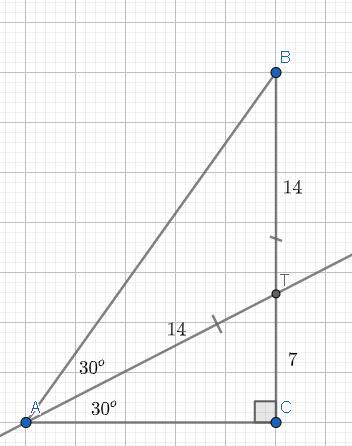
У трикутнику АВС ∟С=90°, ∟А=60°, АТ -
бісектриса трикутника. Знайдіть довжину
катета СВ, якщо ТВ=7 дм.
З МАЛЮНКОМ ЯКЩО БУДЕ I З ОБЬЯСНЕННЯМ БУДЬ ЛАСКА АБО КИНУ РЕПОРТ
Ответы
Ответ дал:
5
<C = 90° ⇒ треугольник ABC — прямоугольный.
<A = 60°; TA — биссектриса угла А, тоесть — этот отрезок делит угол А пополам.
<TAC == <BAT = 60/2 = 30°.
Теорема о 30-градусном угле гласит: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: TC = AT/2 ⇒ AT = TC*2 = 7*2 = 14.
<A = 60° ⇒ <B = 90-60 = 30° ⇒ <B == <BAT = 30° ⇒ AT == BT = 14.
BT = 14; TC = 7 ⇒ BC = 7+14 = 21.
Вывод: BC = 21.
Приложения:
Аноним:
лучшая
у меня в профиле есть еще вопрос по геометрии реши пожалуйста если не сложно
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад