Question

Расстояние от вершины B ромба ABCD до одной из его сторон равно 9, а периметр ромба равен 72. Найдите углы ромба.

Answer 1

Ответ:

30°, 150°, 30°, 150°.

Объяснение:

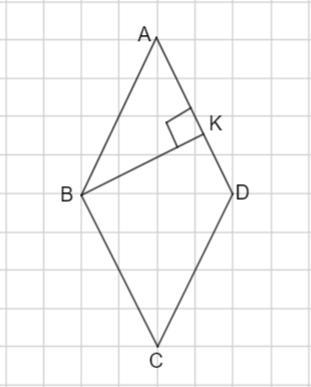
Пусть дан ромб ABCD. Р=72 ед., $BK$⊥$AD$, BK= 9 ед.

Расстояние от вершины В до стороны ромба - это длина пер перпендикуляра ВК.

Периметр ромба определяется по формуле Р=4а, где а -сторона ромба.

Тогда а= 72:4=18 ед.

Рассмотрим треугольник АКВ - прямоугольный. АВ= 18 ед., ВК= 9 ед.

Так как катет прямоугольного треугольника равен половине гипотенузы

$BK=\dfrac{1}{2} AB$ ,

то  угол, лежащий напротив этого катета равен 30°.

Значит, ∠А=30°. У ромба противолежащие углы равны. Тогда ∠С=∠А=30°.

∠С и  ∠D - внутренние односторонние, образованные AD║BC  и секущей CD .

Тогда ∠С +  ∠D =180°. Отсюда следует, что ∠ D=180°-∠C;

∠ D=180°-30°=150°

∠B=∠D=150°