Question

Здравствуйте,даю 90 баллов, помогите сколько сможете решить... Хотя-бы 15 пример

Answer 1

решение примера №15

$\displaystyle \left \{ {{x=2cost} \atop {y=6sint}} \right. ; y\geq 3; y=3$

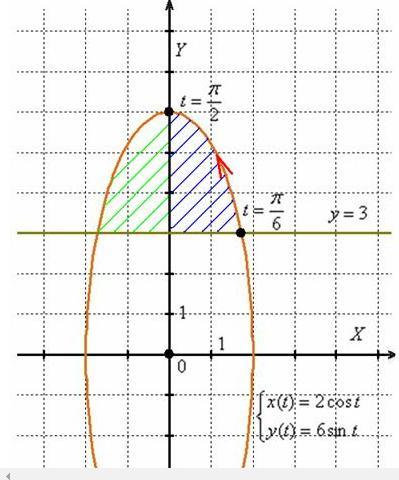
данные параметрические уравнения задают канонический эллипс с центром в начале координат, большой полуосью «2» и малой полуосью «6»

В качестве ориентира найдём несколько точек, которые соответствуют наиболее простым значениям параметра

t=0 ; А(2;0)

t=π/2; B(0;6)

t=π; C=(-2;0)

t=3π/2; D(0;-6)

прямая y=3 пересекает наш эллипс.

найдем точки пересечения

y=3; 3=6sint; sint=1/2; t=π/6 и 5π/6

очевидно что точка π/2 ,будет вершиной нашей фигуры.

тогда можно найти площадь половины от π/6 до π/2

т.к. по условию ограничение дано по у≥3

то площадь будем искать:

$\displaystyle S=2\int\limits^{\pi /2}_{\pi /6} {x(t)*y`(t)} \, dt =2\int\limits^{\pi /2}_{\pi /6} {2cost*(6sint)`} \, dt=24\int\limits^{\pi /2}_{\pi /6} {sin^2t} \, dt =\\\\=24*\frac{1}{2}\int\limits^{\pi /2}_{\pi /6} {(1+cos2t)} \, dt=12(t+\frac{1}{2}sin2t)\bigg|^{\pi /2}_{\pi /6}=\\\\=12(\frac{\pi }{2}+\frac{1}{2}sin\pi -\frac{\pi }{6}-\frac{1}{2}sin\frac{\pi }{3})=12(\frac{\pi }{2}-\frac{\pi }{6}-\frac{\sqrt{3}}{4})=12(\frac{\pi }{3}-\frac{\sqrt{3}}{4})=4\pi -3\sqrt{3}$