Даю 30 баллов!
Найдите расстояние от центра правильного треугольника до его стороны, если его сторона равна 12√3
Ответы
Ответ дал:
1
Ответ:
Расстояние от центра правильного треугольника до его стороны равно ед.
Объяснение:
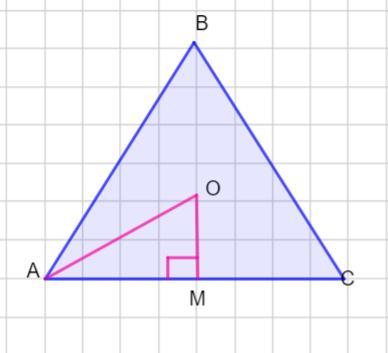
Пусть дан равносторонний Δ АВС со стороной 12√3 ед..
Точка О - центр данного треугольника
Проведем ОМ ⊥ АС.
Центр треугольника находится в точке пересечения медиан, биссектрис и высот.
Тогда точка М - середина стороны АС
ед.
Если треугольник равносторонний, то все углы равны по 60°.
И если точка О - точка пересечения биссектрис, то
∠ОАМ= 30°.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
OM=6 ед.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад