Ответы
Ответ дал:
1
Ответ:
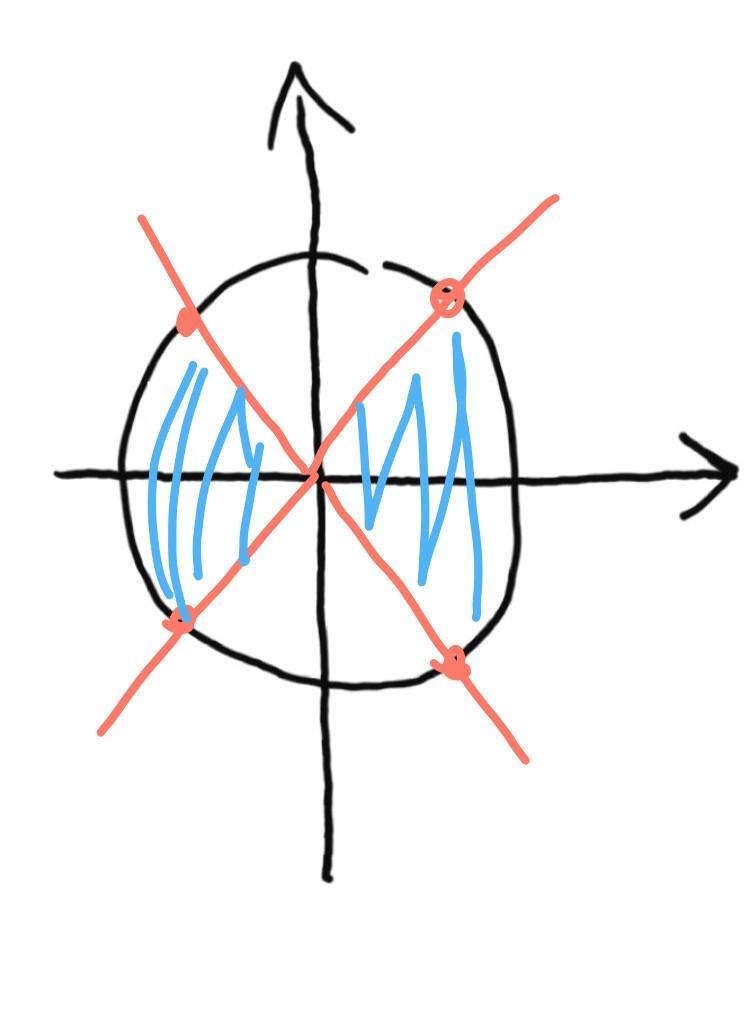
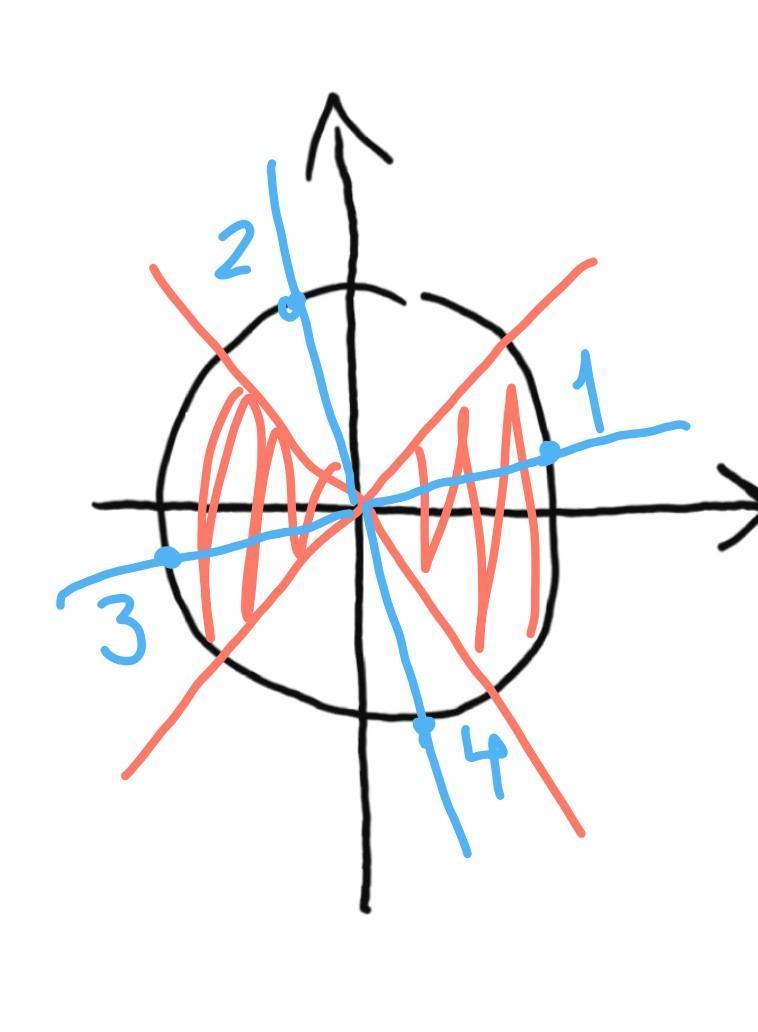
корни 2 и 4 не входят в ОДЗ
Получаем
Ответ:
n принадлежит Z.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад