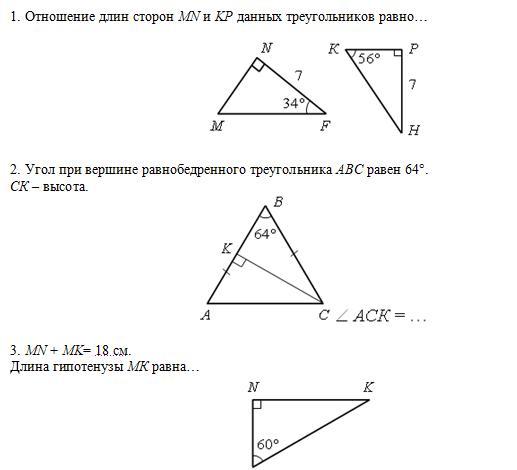
Ответы
1.
<M = 90 - <NPM = 90-34 = 56°
<H = 90 - <PKH = 90-56 = 34°.
Как мы видим, обе треугольника — подобны друг другу, так как имеют равны углы.
Также учтём, то один катет и каждого прямоугольного треугольника — равен 7-и, что и означает, что по 2-ому признаку равенства прямоугольных треугольников — ΔMNP == ΔKPH.
Тоесть: отношение равных катетов равно: .
2.
Треугольник равнобёдренный, что и означает, что боковые стороны равны, что и означает, что углы, противоположные боковым сторонам — равны друг другу, тоесть: <A == <C = (180-(64°))/2 = 58°.
<A = 58°; <AKC = 90° => <ACK = 90-58 = 32°.
Вывод: <ACK = 32°.
3.
<M = 60° => <K = 90-60 = 30°.
Тоерема о 30-градусном угле прямоугольного треугольника таков: Катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: MN = MK/2.
У нас есть 2 условия: МN+МК = 18; MN = MK/2.
Этого нам достаточно, чтобы найт каждый из них — с помощью системы (переменные: MN = x; MK = 2x):
Вывод: MK = 12.