Question

2 Задачи по геометрии

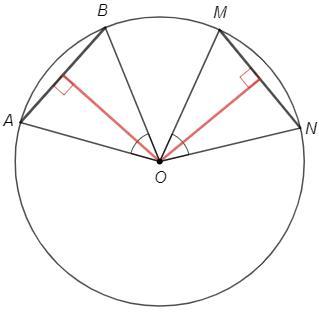
1) Дана окружность. В ней мы взяли две равные хорды AB и MN. Доказать, что расстояние от точки O (центра) до каждой из хорд одинаково

2) Дана окружность. AB диаметр этой окружности. Т. C принадлежит окружности. Доказать, что угол ACB = 90 градусов.

Answer 1

1)

Равные хорды стягивают равные дуги, ∪AB=∪MN

На равные дуги опираются равные центральные углы, ∠AOB=∠MON

Радиусы равны, треугольники AOB и MON равны по двум сторонам и углу между ними.

Высоты равны как соответствующие элементы равных фигур.

В равнобедренном треугольнике высота к основанию является также медианой, то есть расстоянием от вершины (O) до центра основания (AB, MN).

2)

Центральный угол равен дуге, на которую опирается.

Диаметр - развернутый угол - опирается на дугу 180°.

Вписанный угол равен половине дуги, на которую опирается.

Если вписанный угол опирается на диаметр и на дугу 180°, то он равен 180°/2=90°