Question

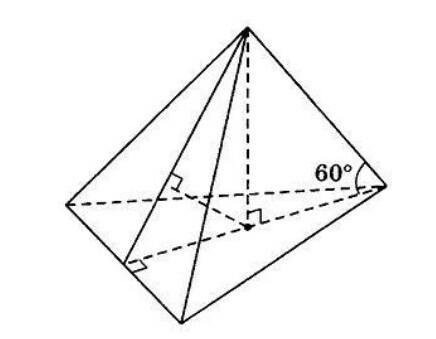
Из основания высоты правильной треугольной пирамиды опущен перпендикуляр длиной 1 на боковую грань. Найдите объём пирамиды, если боковое ребро составляет с плоскостью основания угол 60°.​

Answer 1

Ответ:

$\boldsymbol{\dfrac{13\sqrt{39}}{12}}$

Объяснение:

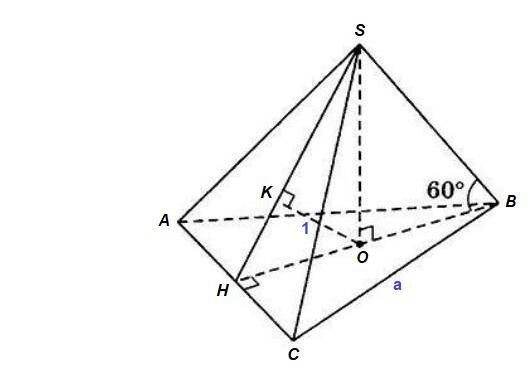
Пирамида правильная, значит в основании правильный треугольник, О - центр вписанной и описанной окружности.

Пусть сторона основания - а.

$OH=\dfrac{a\sqrt{3}}{6}$ как радиус окружности, вписанной в основание.

$OB=\dfrac{a\sqrt{3}}{3}$ как радиус окружности, описанной около основания.

ΔSOB:

   $\dfrac{SO}{OB}=tg60^\circ$

$SO=OB\cdot tg60^\circ=\dfrac{a\sqrt{3}}{3}\cdot \sqrt{3}=a$

ΔHSO: по теореме Пифагора

$SH=\sqrt{SO^2+OH^2}=\sqrt{a^2+\dfrac{3a^2}{36}}=\sqrt{\dfrac{39a^2}{36}}=\dfrac{a\sqrt{39}}{6}$

Высота прямоугольного треугольника с катетами a и b  и гипотенузой с:

$h=\dfrac{ab}{c}$

Из прямоугольного треугольника HSO:

$OK=\dfrac{SO\cdot OH}{SH}=\dfrac{a\cdot\frac{a\sqrt{3}}{6}}{\frac{a\sqrt{39}}{6}}=\dfrac{a\cdot\sqrt{3}\cdot 6}{6\cdot a\sqrt{39}}=\dfrac{a}{\sqrt{13}}$

OK = 1

$\dfrac{a}{\sqrt{13}}=1$

$a=\sqrt{13}$

Площадь основания:

$S=\dfrac{a^2\sqrt{3}}{4}=\dfrac{13\sqrt{3}}{4}$

$V=\dfrac{1}{3}S\cdot SO$

$V=\dfrac{1}{3}\cdot \dfrac{13\sqrt{3}}{4}\cdot \sqrt{13}=\boldsymbol{\dfrac{13\sqrt{39}}{12}}$