Один из углов равнобедренной трапеции равен 150°.
Вычисли площадь трапеции, если её меньшее основание равно 20 см, а боковая сторона равна 12√3 см.
Ответ: площадь трапеции равна
___√____см2.
Ответы
Ответ:
228√3 см²
Объяснение:
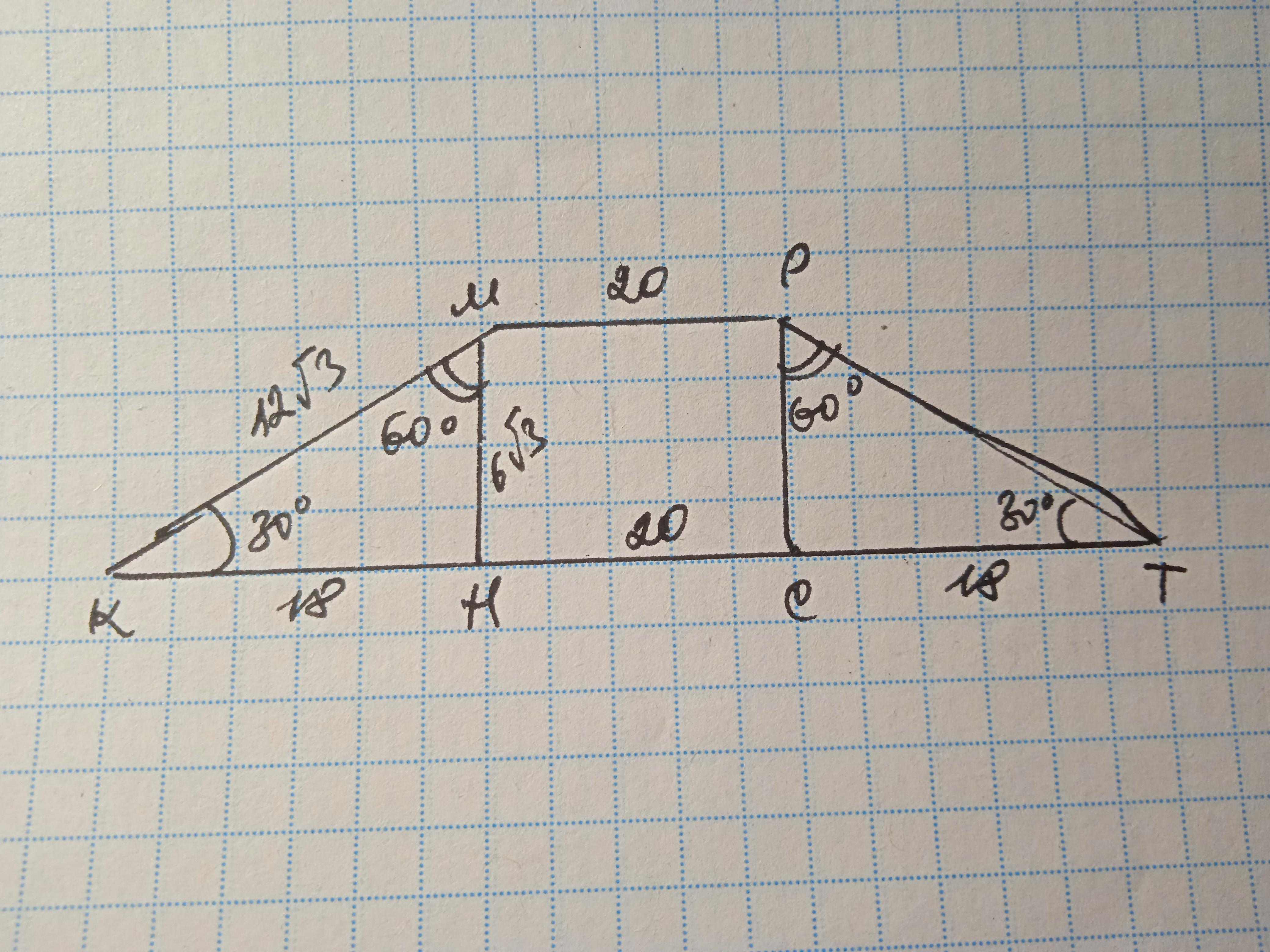
Дано: КМРТ - трапеция, КМ=РТ, ∠КМР=120°, КМ=12√3 см, МР=20 см. Найти S(КМРТ).
Проведем высоты МН и РС. СН=МР=20 см
ΔКМН - прямоугольный, ∠КМН=150-90=60°; ∠К=90-60=30°, значит МН=1/2 КМ=6√3 см.
ΔТРС=ΔКМН по катету и гипотенузе, значит СТ=НК
По теореме Пифагора КН²=КМ²-МН²=432-108=324; КН=СТ=√324=18 см
КТ=18+20+18=56 см.
S=(20+56):2*6√3=38*6√3=228√3 см²
Ответ:
228√3
Объяснение:
У равнобокой трапеции углы при основании равны, значит есть 2 пары углов по 150 и по 180-150. т.е. по 30, боковая сторона 12 корней из 3, а меньшее основание 20, но большее основание равно меньшему основанию + 2 остатка треугольника. Высота - перпендекуляр, следовательно треугольники прямоугольники. катет напротив угла в 30 градусов равен половине гипотенузы, т.е. 6 корней из трех, найдем остаточек треугольника, 12 корней из трех в квадрате минус 6 корней из трех в квадрате равно 144*3-36*3=3(144-36)=3*108=324, корень из 324 - 18, значит этот остаток треугольника 18, значит 2 остатка 36, следовательно большее основание равно 20+36=56, площадь трапеции находится по формуле полусумма оснований на высоту, тогда 56+20=76/2=38* высоту, а высота 6 корней из трех, т.е. 228√3