Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
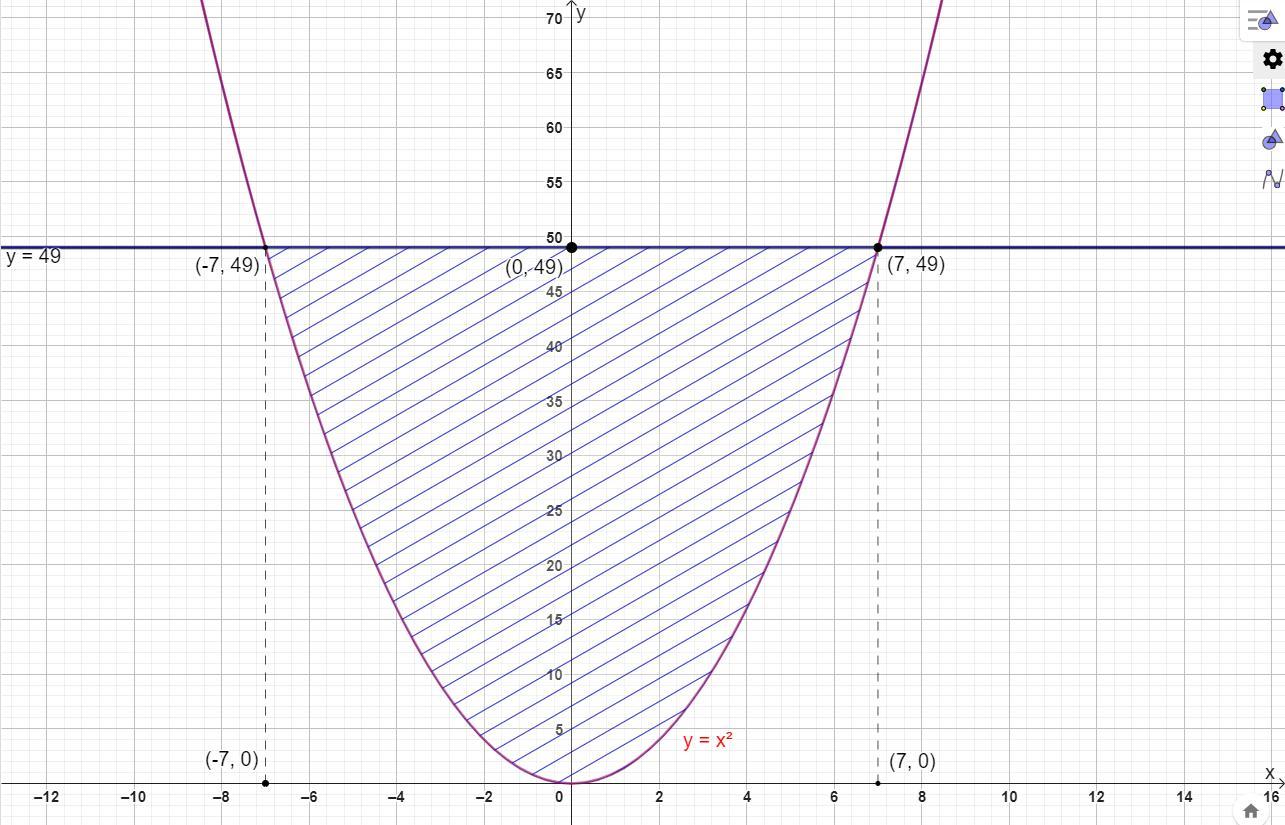
Вычислить площадь фигуры ограниченной заданными линиями
y = x², y = 49
Решение
Найдем абсциссы точек пересечения линий
Получили две точки пересечения (-7;49) и (7;49)
Построим заданные линии.
y = x² - парабола с ветвями направленными вверх и проходящей черех начало координат точкой минимума (0;0)
у = 49 прямая параллельная оси абсцисс через точку (0;49).
График фигуры в файле.
Площадь фигуры будет равна разности площади прямоугольника под прямой y = 49 и под параболой y = 49 в пределах от -7 до 7.
S = Sпр - Sпар
Приложения:
Вас заинтересует
2 года назад
8 лет назад
9 лет назад
9 лет назад