Ответы
Ответ дал:
1
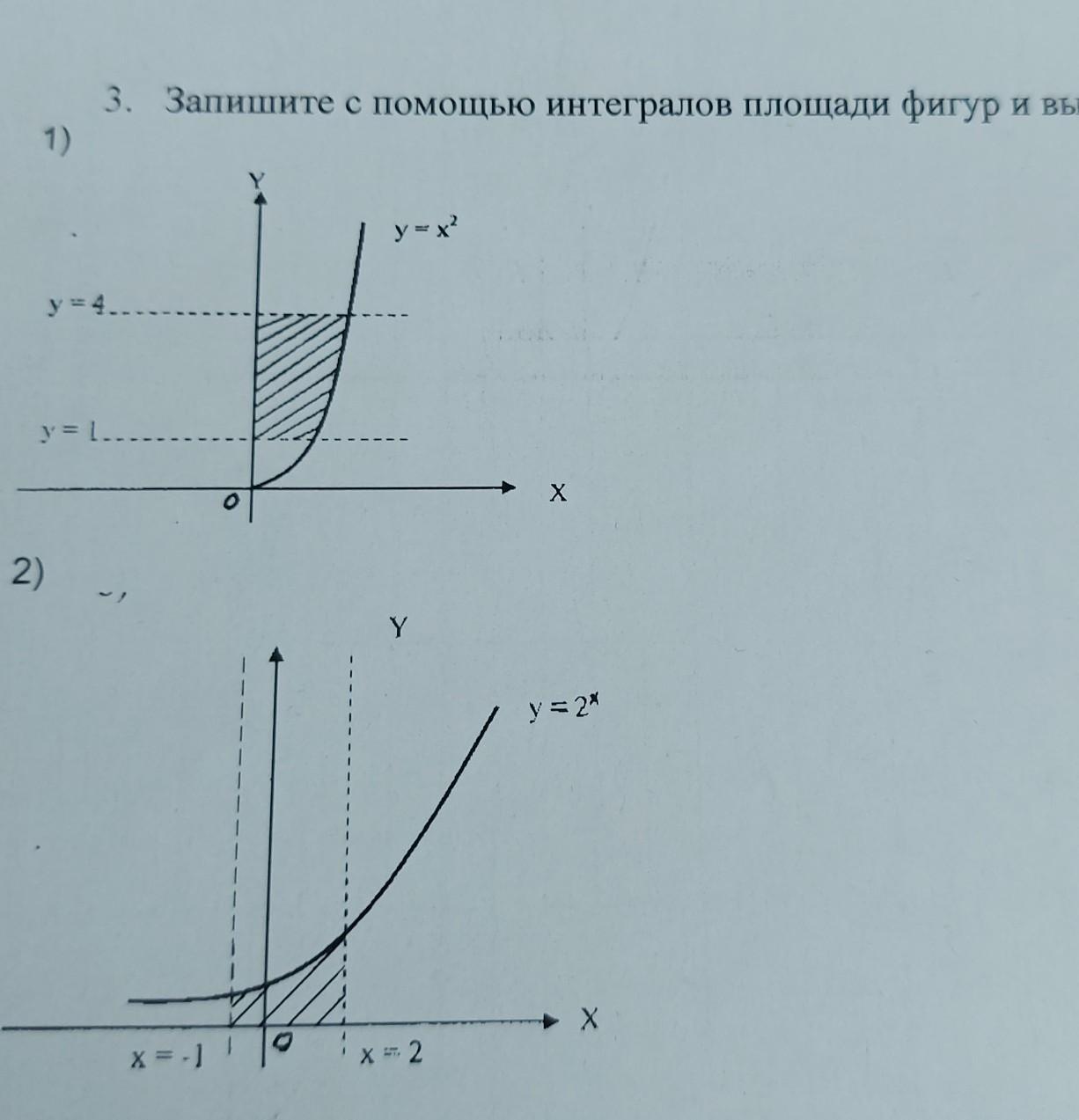
1) Что бы вычислить данную площадь отнимем от всей площади ограниченной y=4 площадь ограниченной y=1
2)
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад