помогите ради христа
Используя основные правила дифференцирования и таблицу производных
основных элементарных функций, найти производную для функции
y=y(x)=f(x);
Приложения:
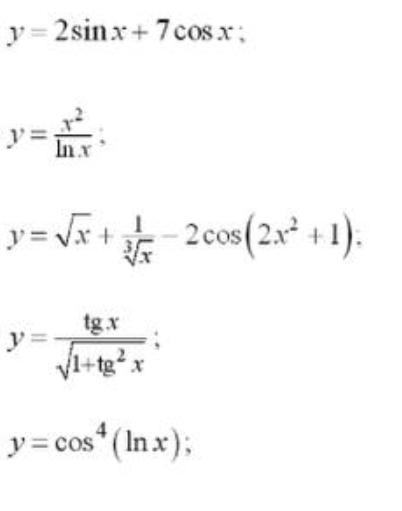
Ответы
Ответ дал:
0
Ответ:
1
2
3
4
5
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад