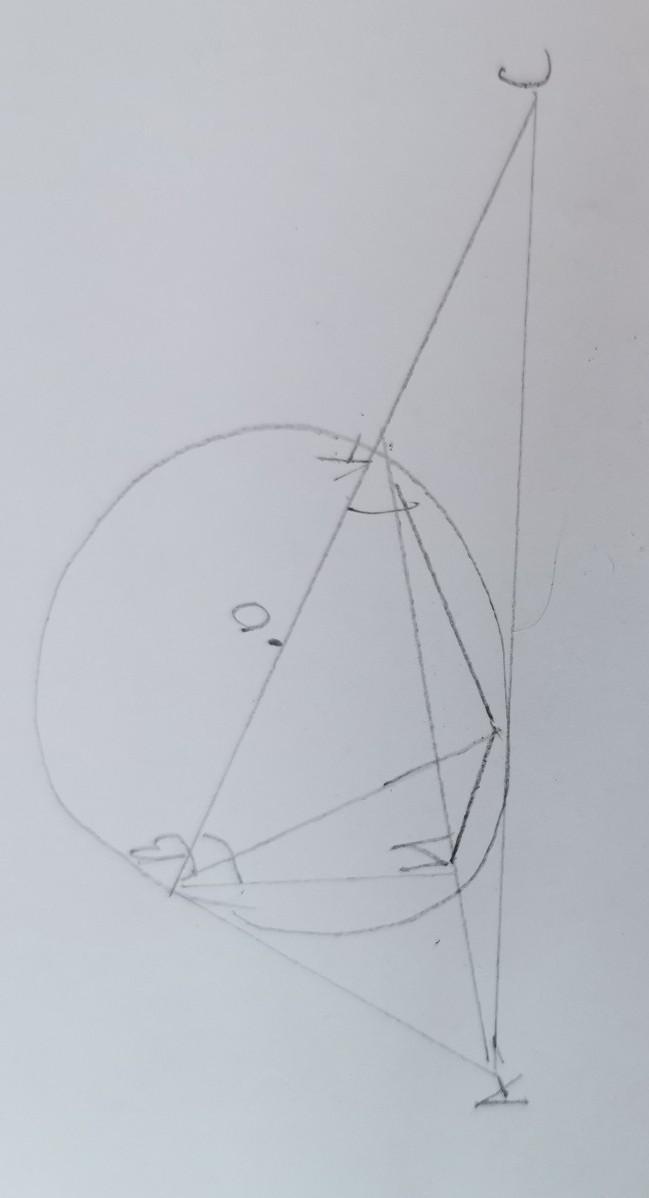
В треугольнике ABC точка M- середина стороны AC. На стороне BC взяли точку K так, что угол BMK прямой. Оказалось, что BK=AB. Найдите BKM , если A + С = 70.
Приложения:

Ответы
Ответ дал:
0
Решение:Опустим в ΔАВМ (АВ = ВК) высоту ВН ⇒ ВН⊥АК, АН = НК, но АМ = МС ⇒ НМ - средняя линия ΔАСК, НМ || ВС. Отрезок ВК из точек Н и М под прямым углом ⇒ четырёхугольник ВКМН вписанный, но НМ || ВК ⇒ ВКМН - равнобедренная трапеция, ВН = МК, ВМ = НК = АН, ∠ВКМ = ∠КВН = (180° - ∠А - ∠С)/2 =55°
Ответ:55°.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад