Question

8 номер, срочно. подробный ответ нужен

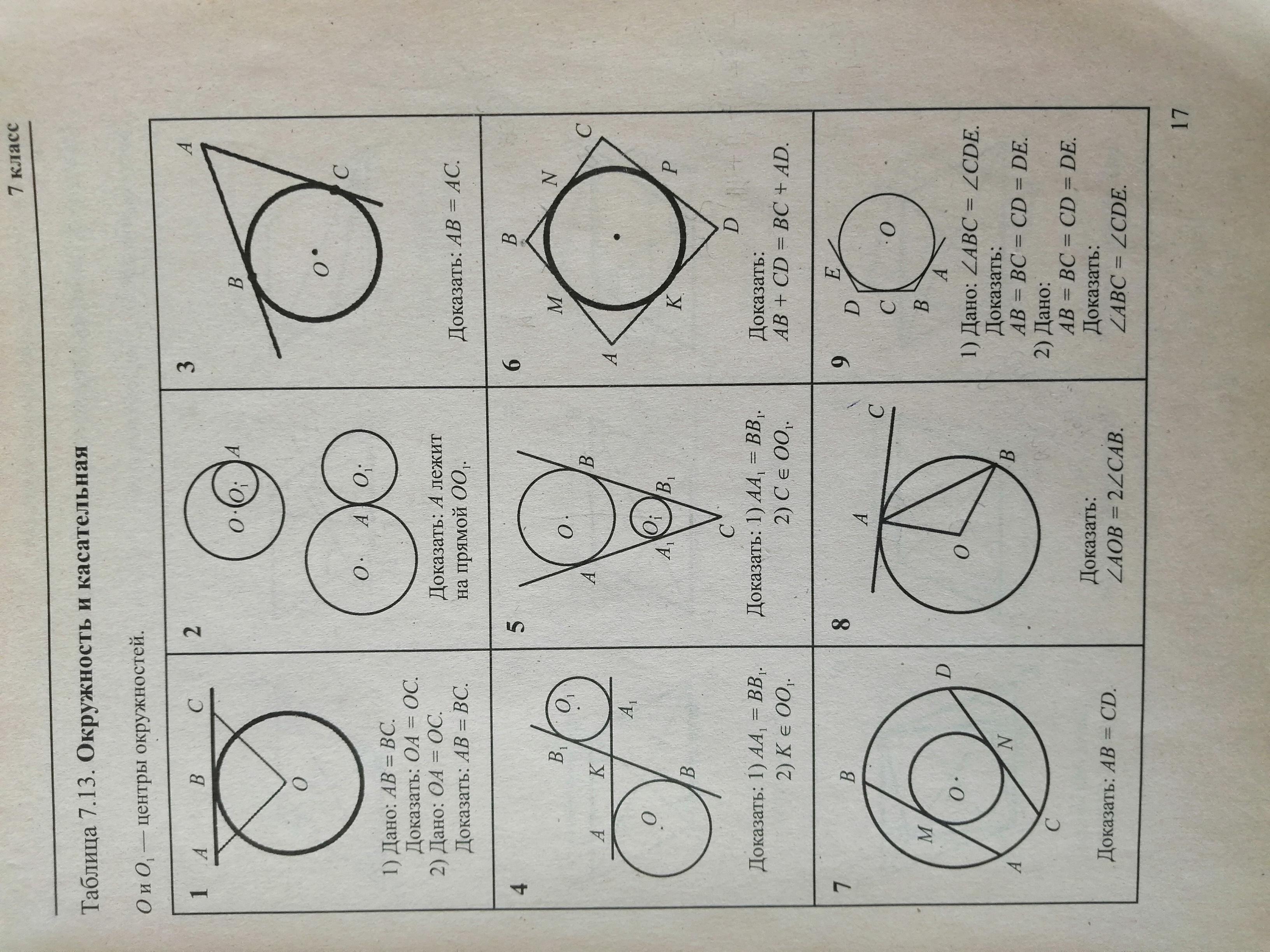
Answer 1

Рассмотрим ΔАОВ:

ОА = ОВ = r - радиус окружности (т.к. О - центр окружности по условию).

Следовательно:

ΔАОВ - равнобедренный:

<OAB = <OBA

Тогда:

<AOB + 2•<OAB = 180° (1)

Рассмотрим прямую АС:

АС является касательной к окружности в точке А. Значит ОА _|_ АС, и тогда:

<ОАС = <ОАВ + <ВАС = 90° (2)

Найдем <ОАВ из (2) и поставим в (1):

<АОВ + 2•(90° - <ВАС) = 180°

<АОВ + 180° - 2•<ВАС = 180°

<АОВ = 2•<ВАС

Что и требовалось доказать!