Помогите пaжалуйста
Из точки А вне окружности проведена секущая, пересекающая окружность в точках В и С. Расстояние от данной точки А до центра окружности равно 7 см. Найдите радиус окружности, если AB=3см, BC=5см.
orjabinina:
Есть свойство для " Секущих, проведённые из одной точки вне круга "- ЗНАЕШЬ?
а что-то случилось? мне просто ответ на задачу нужен.
Могли вместе разобраться. Ответ такой r=5 или r=3
я не шарю, поэтому и задал вопрос. Сорян
Ответы
Ответ дал:
0
Квадрат касательной равен произведению секущей на ее внешнюю часть. Следовательно, для данной точки (A) произведение любой секущей на ее внешнюю часть - число постоянное.
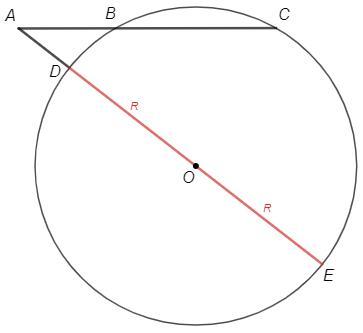
O - центр окружности.
Пусть прямая AO пересекает окружность в точках D и E.
AС - секущая, AB - ее внешняя часть.
AE - секущая, AD - ее внешняя часть.
AC*AB =AE*AD
OD=OE =R (радиусы)
AE =AO+OE =7+R
AD =AO-OD =7-R
AC*AB =AE*AD => 8*3 =(7+R)(7-R) => 49 -R^2 =24 => R =√25 =5 (см)
Приложения:
AB=5, BC=3 /////8*5 =(7+R)(7-R) => 49 -R^2 =40 => R =√9 =3 (см)
по-моему, только одно решение
Давайте голосовать.................
чего-то не пойму, дано AB=3, BC=5
точка А вне окружности
Вы правы. А я д.б. ( плохо читала условие).
Прошу, помогите пожалуйста. Первое задание в профиле или вот ссылка https://znanija.com/task/43728258
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад