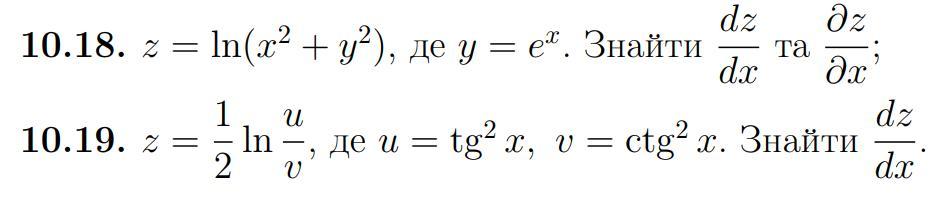Ответы
Ответ дал:
1
10.18
10.19
(в правой части закруглённые d. Внизу, соответственно, тоже)
neeeewakk:
помогите с задачей у меня в профиле
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад