Question

В треугольнике MNP угол M=46. Прямые, содержащие биссектрисы внешних углов при вершинах N и P треугольника MNP, пересекаются в точке S. Найдите угол NSP

Answer 1

Ответ:

как то так.............

Answer 2

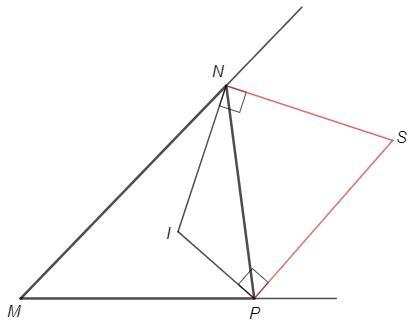
I - точка пересечения внутренних биссектрис

S - точка пересечения внешних биссектрис

∠M+∠N+∠P =180 => ∠M/2 +∠N/2 +∠P/2 =90

∠I +∠N/2 +∠P/2 =180 => ∠I =90 +∠M/2 (угол между внутренними биссектрисами)

Биссектрисы смежных углов перпендикулярны.

В INSP сумма противоположных углов 180.

∠S =180 -∠I =90 -∠M/2 (угол между внешними биссектрисами)

S =90 -46/2 =67°