Question

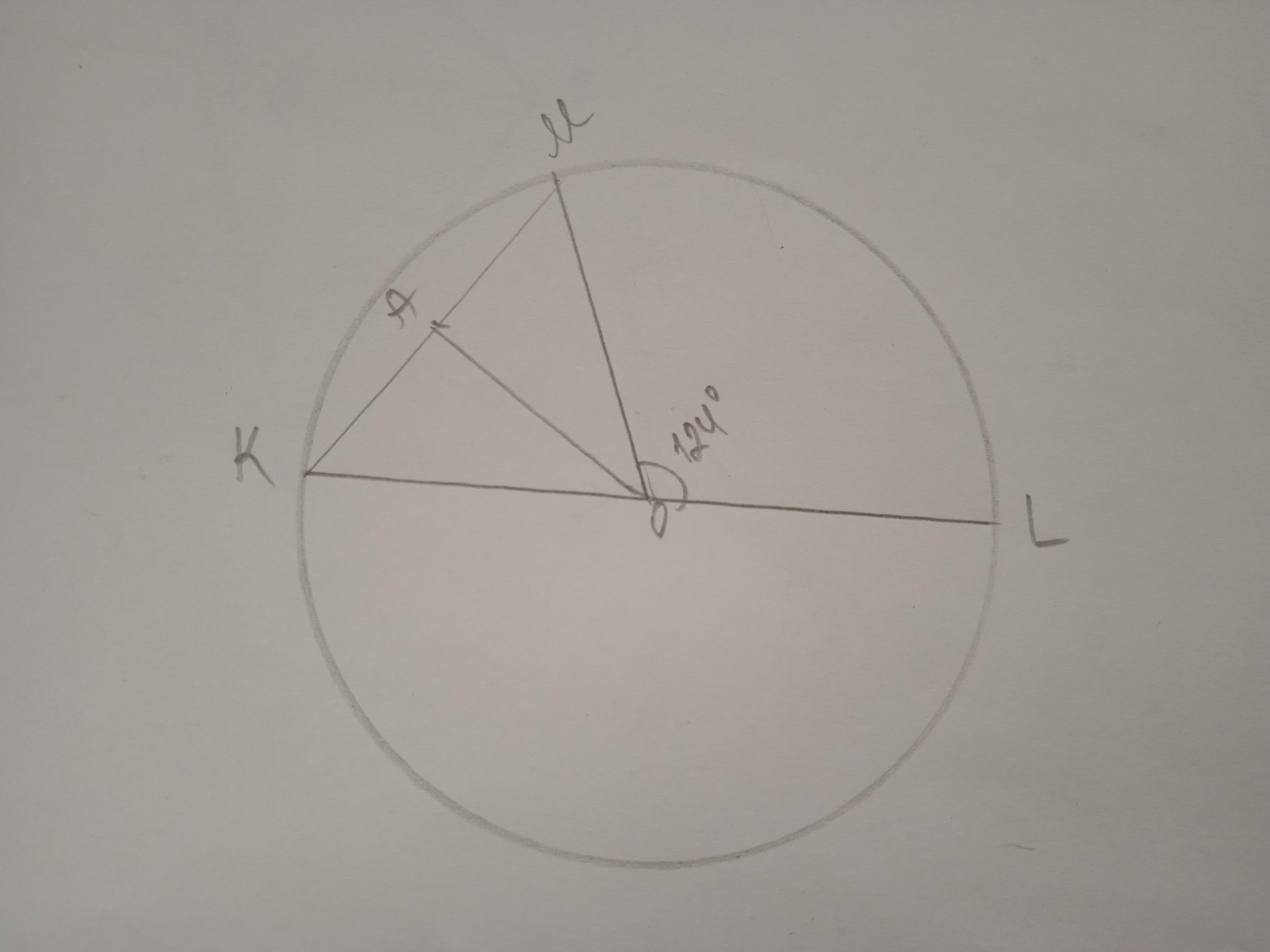
KL - діаметр кола з центром O, MK - хорда, кут LOM = 124 градуса. Знайдiть величину кута MOA, якщо A - середина хорди
СРОЧНО 90 БАЛОВ!

Answer 1

Ответ:

28°

Пошаговое объяснение:

∠КОМ=180-124=56° за властивістю суміжних кутів

ΔАКО=ΔАМО (КА=АМ,  КО=ОМ як радіуси,  АО - спільна сторона)

отже ∠КОА=∠МОА=56:2=28°

Answer 2

Ответ:

28°

Пошаговое объяснение:

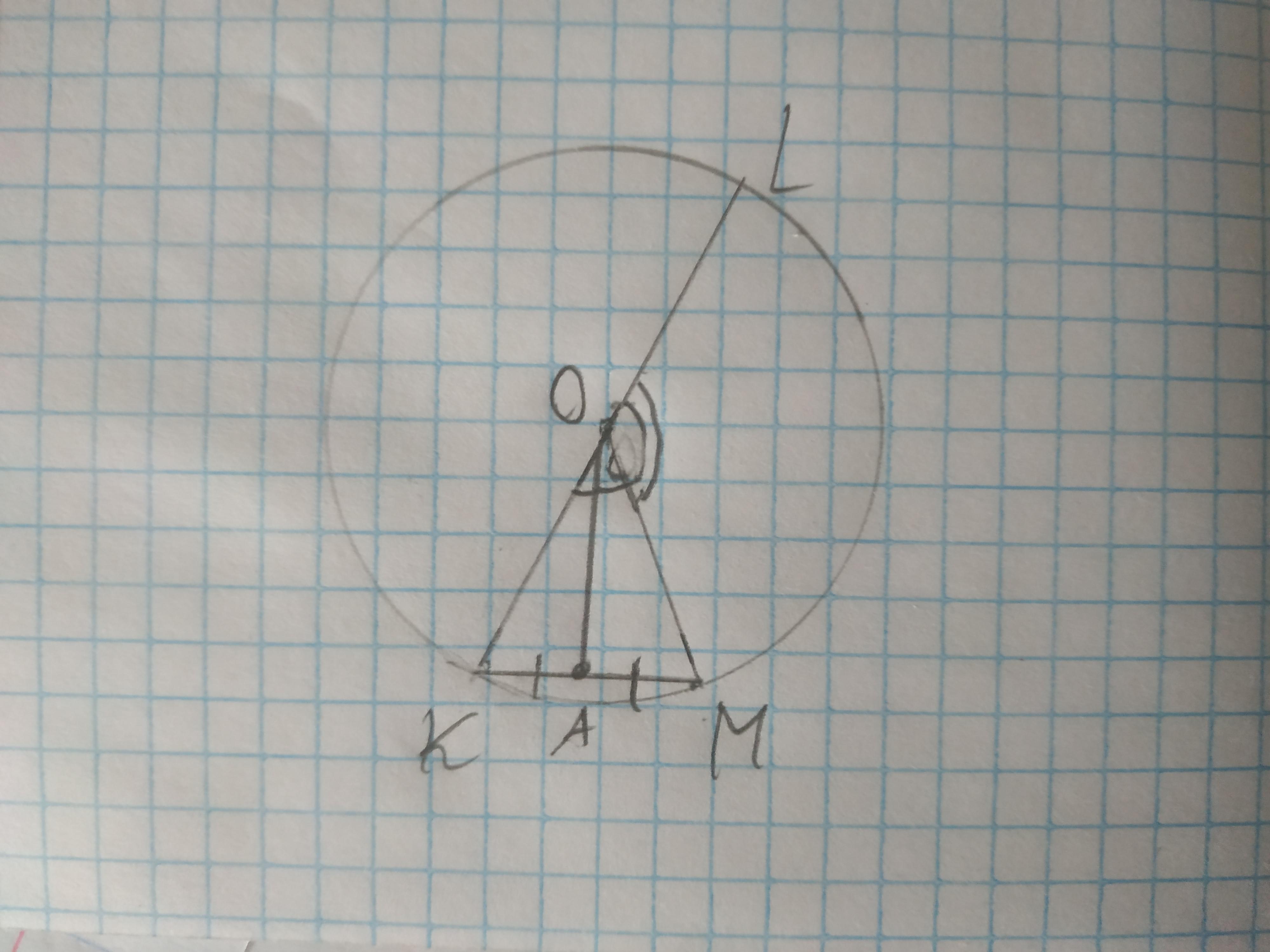
Малюнок прикріплений ( кривий, но зрозуміти можна).

Якщо кут LOM дорівнює 124 градуси, то на кут KOM залишається (180-124) 56 градусів.

OK і OM - радіуси кола, звідси : трикутник KOM - рівнобедрений.

Точка А - середина хорди KM: KA=AM.

Тоді OA - медіана, проведена з вершини рівнобедреного трикутника до основи.

З властивостей рівнобедреного трикутника: OA - медіана, висота і бісектриса одночасно.

Тодік кут MOA дорівнює половині кута KOM

Кут MOA дорівнює 28 градусів.